Lösung 2.2:9a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
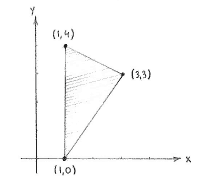
We can start by drawing the points
+
We can start by drawing the points (1,4), (3,3) and (1,0) in a coordinate system and draw lines between them, so that we get a picture of how the triangle looks like.
-
<math>\left( 1 \right.,\left. 4 \right)</math>,
+
 
-
<math>\left( 3 \right.,\left. 3 \right)</math>
+
-
and
+
-
<math>\left( 1 \right.,\left. 0 \right)</math>
+
-
in a coordinate system and draw lines between them, so that we get a picture of how thetriangle looks.
+
-
{{NAVCONTENT_START}}
 
[[Image:2_2_9_a-1(2).gif|center]]
[[Image:2_2_9_a-1(2).gif|center]]
-
{{NAVCONTENT_STOP}}
 
If we now think of how we should use the fact that the area of a triangle is given by the formula
If we now think of how we should use the fact that the area of a triangle is given by the formula
-
Area=
+
{{Displayed math||<math>\text{Area} = \frac{1}{2}\cdot\text{(base)}\cdot\text{(height),}</math>}}
-
<math>\frac{1}{2}</math>
+
-
(base)∙(height),
+
-
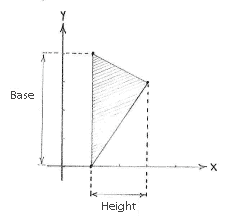
it is clear that it is most appropriate to use the edge from
+
it is clear that it is most appropriate to use the edge from (1,0) to (1,4) as the base of the triangle. The base is then parallel with the ''y''-axis and we can read off its length as the difference in the ''y''-coordinate between the corner points (1,0) and (1,4), i.e.
-
<math>\left( 1 \right.,\left. 0 \right)</math>
+
-
to
+
-
<math>\left( 1 \right.,\left. 4 \right)</math>
+
-
as the base of the triangle.
+
-
The base is then parallel with the y-axis and we can read off its length as the difference in the
+
-
<math>y</math>
+
{{Displayed math||<math>\text{base} = 4-0 = 4\,\textrm{.}</math>}}
-
-coordinate between the corner points
+
-
<math>\left( 1 \right.,\left. 0 \right)</math>
+
-
and
+
-
<math>\left( 1 \right.,\left. 4 \right)</math>, i.e.
+
-
base
+
In addition, the triangle's height is the horizontal distance from the third corner point (3,3) to the base and we can read that off as the difference in the ''x''-direction between (3,3) and the line <math>x=1</math>, i.e.
-
<math>=4-0=0</math>.
+
-
In addition, the triangle's height is the horizontal distance from the third corner point
+
-
<math>\left( 3 \right.,\left. 3 \right)</math>
+
-
to the base and we can read that off as the difference in the
+
-
<math>x</math>
+
-
-direction between
+
-
<math>\left( 3 \right.,\left. 3 \right)</math>
+
-
and the line
+
-
<math>x=1</math>, i.e.
+
-
height
+
{{Displayed math||<math>\text{height} = 3-1 = 2\,\textrm{.}</math>}}
-
<math>=3-1=2</math>.
+
-
{{NAVCONTENT_START}}
 
[[Image:2_2_9_a-2(2).gif|center]]
[[Image:2_2_9_a-2(2).gif|center]]
-
{{NAVCONTENT_STOP}}
 
Thus, the triangle's area is
Thus, the triangle's area is
-
Area=
+
{{Displayed math||<math>\text{Area} = \tfrac{1}{2}\cdot\textrm{(base)}\cdot\textrm{(height)} = \tfrac{1}{2}\cdot 4\cdot 2 = 4\,\text{u.a.}</math>}}
-
<math>\frac{1}{2}</math>
+
-
(base)∙(height)
+
-
<math>=\frac{1}{2}\centerdot 4\centerdot 2=4</math>
+
-
= area units.
+

Version vom 13:58, 24. Sep. 2008

We can start by drawing the points (1,4), (3,3) and (1,0) in a coordinate system and draw lines between them, so that we get a picture of how the triangle looks like.



If we now think of how we should use the fact that the area of a triangle is given by the formula

Vorlage:Displayed math

it is clear that it is most appropriate to use the edge from (1,0) to (1,4) as the base of the triangle. The base is then parallel with the y-axis and we can read off its length as the difference in the y-coordinate between the corner points (1,0) and (1,4), i.e.

Vorlage:Displayed math

In addition, the triangle's height is the horizontal distance from the third corner point (3,3) to the base and we can read that off as the difference in the x-direction between (3,3) and the line \displaystyle x=1, i.e.

Vorlage:Displayed math



Thus, the triangle's area is

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:9a“