Lösung 2.3:10b
Aus Online Mathematik Brückenkurs 1
K (Lösning 2.3:10b moved to Solution 2.3:10b: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
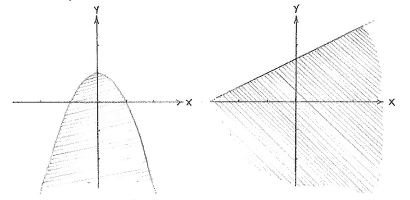
| - | {{ | + | The inequality |
| - | + | <math>y\le \text{1}-x^{\text{2}}</math> | |
| - | { | + | defines the area under and on the curve |
| - | {{ | + | <math>y=\text{1}-x^{\text{2}}</math>, which is a parabola with a maximum at |
| - | < | + | <math>\left( 0 \right.,\left. 1 \right)</math>. We can rewrite the other inequality |
| - | {{ | + | <math>x\ge \text{ 2}y-\text{3}</math> |
| - | {{ | + | as |
| - | + | <math>y\le \text{ }{x}/{2}\;+{3}/{2}\;</math> | |
| - | {{ | + | and it defines the area under and on the straight line |
| + | <math>y=\text{ }{x}/{2}\;+{3}/{2}\;</math>. | ||
| + | |||
| + | |||
[[Image:2_3_10_b1.gif|center]] | [[Image:2_3_10_b1.gif|center]] | ||
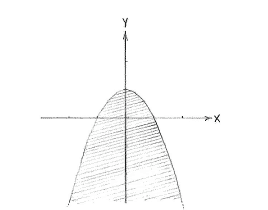
| + | Of the figures above, it seems that the region associated with the parabola lies completely under the line | ||
| + | <math>y=\text{ }{x}/{2}\;+{3}/{2}\;</math> | ||
| + | and this means that the area under the parabola satisfies both inequalities. | ||
| + | |||
[[Image:2_3_10_b2.gif|center]] | [[Image:2_3_10_b2.gif|center]] | ||
| + | |||
| + | NOTE: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the | ||
| + | <math>y</math> | ||
| + | -values on the line | ||
| + | <math>y_{\text{line}}=\text{ }{x}/{2}\;+{3}/{2}\;</math> | ||
| + | is always larger than the corresponding | ||
| + | <math>y</math> | ||
| + | -value on the parabola | ||
| + | <math>y_{\text{parabola}}=\text{1}-x^{\text{2}}</math> | ||
| + | by studying the difference between them: | ||
| + | |||
| + | |||
| + | <math>y_{\text{line}}-y_{\text{parabola}}=\text{ }\frac{x}{2}+\frac{3}{2}-\left( \text{1}-x^{\text{2}} \right)</math> | ||
| + | |||
| + | |||
| + | If this difference is positive regardless of how | ||
| + | <math>x</math> | ||
| + | is chosen, then we know that the line's | ||
| + | <math>y</math> | ||
| + | -value is always greater than the parabola's | ||
| + | <math>y</math> | ||
| + | -value. After a little simplification and completing the square, we have | ||
| + | |||
| + | |||
| + | <math>\begin{align} | ||
| + | & y_{\text{line}}-y_{\text{parabola}}=\text{ }\frac{x}{2}+\frac{3}{2}-\left( \text{1}-x^{\text{2}} \right)=x^{2}+\frac{1}{2}x+\frac{1}{2} \\ | ||
| + | & =\left( x+\frac{1}{4} \right)^{2}-\left( \frac{1}{4} \right)^{2}+\frac{1}{2}=\left( x+\frac{1}{4} \right)^{2}+\frac{7}{16} \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | |||
| + | and this expression is always positive because | ||
| + | <math>\frac{7}{16}</math> | ||
| + | is a positive number and | ||
| + | <math>\left( x+\frac{1}{4} \right)^{2}</math> | ||
| + | is a quadratic which is never negative. In other words, the parabola is completely under the line. | ||
Version vom 12:39, 21. Sep. 2008
The inequality \displaystyle y\le \text{1}-x^{\text{2}} defines the area under and on the curve \displaystyle y=\text{1}-x^{\text{2}}, which is a parabola with a maximum at \displaystyle \left( 0 \right.,\left. 1 \right). We can rewrite the other inequality \displaystyle x\ge \text{ 2}y-\text{3} as \displaystyle y\le \text{ }{x}/{2}\;+{3}/{2}\; and it defines the area under and on the straight line \displaystyle y=\text{ }{x}/{2}\;+{3}/{2}\;.
Of the figures above, it seems that the region associated with the parabola lies completely under the line \displaystyle y=\text{ }{x}/{2}\;+{3}/{2}\; and this means that the area under the parabola satisfies both inequalities.
NOTE: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the \displaystyle y -values on the line \displaystyle y_{\text{line}}=\text{ }{x}/{2}\;+{3}/{2}\; is always larger than the corresponding \displaystyle y -value on the parabola \displaystyle y_{\text{parabola}}=\text{1}-x^{\text{2}} by studying the difference between them:
\displaystyle y_{\text{line}}-y_{\text{parabola}}=\text{ }\frac{x}{2}+\frac{3}{2}-\left( \text{1}-x^{\text{2}} \right)
If this difference is positive regardless of how
\displaystyle x
is chosen, then we know that the line's
\displaystyle y
-value is always greater than the parabola's
\displaystyle y
-value. After a little simplification and completing the square, we have
\displaystyle \begin{align}
& y_{\text{line}}-y_{\text{parabola}}=\text{ }\frac{x}{2}+\frac{3}{2}-\left( \text{1}-x^{\text{2}} \right)=x^{2}+\frac{1}{2}x+\frac{1}{2} \\
& =\left( x+\frac{1}{4} \right)^{2}-\left( \frac{1}{4} \right)^{2}+\frac{1}{2}=\left( x+\frac{1}{4} \right)^{2}+\frac{7}{16} \\
\end{align}
and this expression is always positive because
\displaystyle \frac{7}{16}
is a positive number and
\displaystyle \left( x+\frac{1}{4} \right)^{2}
is a quadratic which is never negative. In other words, the parabola is completely under the line.