Lösung 2.3:6a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 2.3:6a moved to Solution 2.3:6a: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Using the squaring rule, we recognize the polynomial as the expansion of
-
<center> [[Image:2_3_6a.gif]] </center>
+
<math>\left( x-1 \right)^{2}</math>,
-
{{NAVCONTENT_STOP}}
+
 
 +
 
 +
<math>x^{2}-2x+1=\left( x-1 \right)^{2}</math>
 +
 
 +
 
 +
This quadratic expression has its smallest value, zero, when
 +
<math>x-\text{1}=0</math>, i.e.
 +
<math>x=\text{1}</math>. All non-zero values of
 +
<math>x-\text{1}</math>
 +
give a positive value for
 +
<math>\left( x-1 \right)^{2}</math>.
 +
 
 +
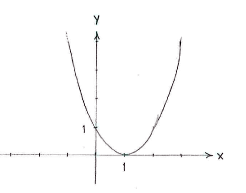
NOTE: If we draw the curve
 +
<math>y=\left( x-1 \right)^{2}</math>, we see that it has a minimum value of zero at
 +
<math>x=\text{1}</math>.
 +
 
 +
 
[[Image:2_3_6_a.gif|center]]
[[Image:2_3_6_a.gif|center]]

Version vom 10:51, 21. Sep. 2008

Using the squaring rule, we recognize the polynomial as the expansion of \displaystyle \left( x-1 \right)^{2},


\displaystyle x^{2}-2x+1=\left( x-1 \right)^{2}


This quadratic expression has its smallest value, zero, when \displaystyle x-\text{1}=0, i.e. \displaystyle x=\text{1}. All non-zero values of \displaystyle x-\text{1} give a positive value for \displaystyle \left( x-1 \right)^{2}.

NOTE: If we draw the curve \displaystyle y=\left( x-1 \right)^{2}, we see that it has a minimum value of zero at \displaystyle x=\text{1}.


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:6a“