Lösung 2.2:5b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 2.2:5b moved to Solution 2.2:5b: Robot: moved page)
Zeile 1: Zeile 1:
 +
Because the straight line is to have a gradient of
 +
<math>-3</math>, its equation can be written as
 +
 +
 +
<math>y=-3x+m</math>
 +
 +
 +
where
 +
<math>m</math>
 +
is a constant. If the line is also to pass through the point
 +
<math>\left( x \right.,\left. y \right)=\left( 1 \right.,\left. -2 \right)</math>, the point
 +
must satisfy the equation of the line
 +
 +
 +
<math>-2=-3\centerdot 1+m</math>
 +
 +
 +
which gives that
 +
<math>m=1</math>.
 +
 +
The answer is thus that the equation of the line is
 +
<math>y=-3x+1</math>.
 +
 +
{{NAVCONTENT_START}}
{{NAVCONTENT_START}}
-
<center> [[Image:2_2_5b.gif]] </center>
+
 
[[Image:1_2_2_5_b_ss1.jpg|center|300px]]
[[Image:1_2_2_5_b_ss1.jpg|center|300px]]
{{NAVCONTENT_STOP}}
{{NAVCONTENT_STOP}}

Version vom 09:13, 18. Sep. 2008

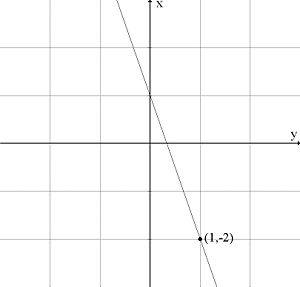
Because the straight line is to have a gradient of \displaystyle -3, its equation can be written as


\displaystyle y=-3x+m


where \displaystyle m is a constant. If the line is also to pass through the point \displaystyle \left( x \right.,\left. y \right)=\left( 1 \right.,\left. -2 \right), the point must satisfy the equation of the line


\displaystyle -2=-3\centerdot 1+m


which gives that \displaystyle m=1.

The answer is thus that the equation of the line is \displaystyle y=-3x+1.


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:5b“