2. Algebra
Aus Online Mathematik Brückenkurs 1
(Ny sida: __NOTOC__ <!-- Don't remove this line --> <!-- A hack to get a popup-window --> {|align="left" | width="220" height="203" |<math>\text{@(a class="image" href="http://smaug.nti.se/temp/KT...) |
|||
| Zeile 9: | Zeile 9: | ||
|} | |} | ||
| - | ''' | + | '''Why do we use letters letters and who were the first to do this? ''' |
| - | '' | + | ''Watch the video in which the lecturer Lasse Svensson tells us how algebra |
| + | developed and answers Elins questions about Part 2 of the course. | ||
| Zeile 23: | Zeile 24: | ||
| - | Algebra | + | Algebra is the branch of mathematics which works with symbolic expressions and variables, and not just calculations with numbers. |
| - | Algebra | + | Algebra is needed in many situations. For example algebra can be used to describe mathematical problems and to solve equations. Among other things it can describe geometric facts by means of algebraic statements, and many problems can be resolved with the help of algebraic operations. |
| + | In some cases the value of an expression does not simplify to a numeric value. The reason may be that the expression includes unknown parameters or variables. It may also be that it is important that a number be exactly specified, such as that given circle is to have a circumference of exactly <math>4\pi</math> units, or the hypotenuse of a triangle is to b e<math>\sqrt{3}</math>, or even that the value of a constant is to be <math>\dfrac{1-\ln 2}{3}</math>. | ||
| - | I en del fall kan man inte räkna ut värdet av ett uttryck till ett numeriskt värde. Anledningen kan vara att uttrycket innehåller obekanta parametrar eller variabler. Det kan också vara så att det är viktigt att ett tal är exakt angivet, t.ex. att en viss cirkel har en omkrets som är exakt <math>4\pi</math>, eller hypotenusans längd för en triangel är <math>\sqrt{3}</math>, eller varför inte att värdet på en konstant är <math>\dfrac{1-\ln 2}{3}</math>. | ||
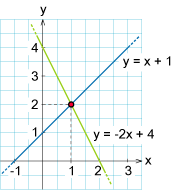
| + | [[Bild:grafisk lösning.gif|thumb|250px|A linear equation with two unknowns can be interpreted as a straight line in a coordinate system. The common solution (''x'',''y'') to these two equations corresponds to the common point of these lines, that is their point of intersection. ]] | ||
| + | Then it may be easier just to call the number, for example, ''a''. In return, you must accept that you may not arrive at a numerical value, but instead may finish up with an expression that contains ''a''. | ||
| - | + | A common situation where it algebra may be necessary is simplification. It is often very important to simplify an expression, such as before differentiation, or when an equation is to be solved. | |
| - | + | ||
| - | En vanlig situation där man kan behöva algebra är förenkling. Det är ofta mycket viktigt att förenkla ett uttryck, t.ex. innan man skall derivera, eller när man löser en ekvation. | ||
| + | Simplification reduces the risk of careless mistakes and avoids unnecessary work. To simplify means to transform an expression from one form to another. Which of these are considered as ”simple”is sometimes obvious, but it can also depend on what you want to do with the expression. | ||
| - | + | When differentiating, it may be advantageous to transform the expression into a sum of a number of terms. On the other hand when we solve an equation, it may be advantageous to reformulate the expression as a product of a number of factors. Therefore, one needs to be proficient in converting expressions into different forms. | |
| - | + | '''It is important to note that the material in this section— as well as in other parts of the course — is designed that one does not use calculators.''' | |
| - | + | ''When you get to university, you will not be allowed to use calculators during your "exams" at least this is true for the basic courses.'' | |
| - | '' | + | |
| - | + | ||
| - | + | ||
<div class="inforuta"> | <div class="inforuta"> | ||
| - | ''' | + | '''To succeed you with Algebra''' |
| - | # | + | # Start by reading the section's theory and study the examples. |
| - | # | + | #Work through the practice questions and try to solve them without using a calculator. Make sure that you have the right answer by clicking on the answer button. If you do not have it, you can click on the solution button to see what went wrong |
| - | # | + | #Then go ahead and answer the questions in the basic test of the section. |
| - | # | + | # If you get stuck on a point, check to see if someone else has discussed the point in the forum belonging to the section. If not, take up the point yourself. Your teacher (or a student) will respond to your question within a few hours. |
| - | # | + | #When you are finished with the exercises and the basic test in a section you should take the final test to get a pass for the section. The requirement here is to answer correctly three questions in a row before you can move on to the next section. |
| - | # | + | # When you have answered correctly all questions in both the basic and the final test of this section you will have a pass for this section and can move on to Part 3 of the course. |
| - | PS. | + | PS. If you feel that you are very familiar with the contents of a section you can test yourself by going directly to the basic and final tests. You must answer all the questions correctly in a test, but you may do the test several times if you do not succeed at the first attempt. It is your final results which appear in the statistics. |
</div> | </div> | ||
Version vom 13:48, 10. Jul. 2008
| \displaystyle \text{@(a class="image" href="http://smaug.nti.se/temp/KTH/film4.html" target="_blank")@(img src="http://wiki.math.se/wikis/2008/forberedandematte1/img_auth.php/0/00/Lars_och_Elin.jpg" alt="Film om algebra")@(/img)@(/a)} |
Why do we use letters letters and who were the first to do this?
Watch the video in which the lecturer Lasse Svensson tells us how algebra
developed and answers Elins questions about Part 2 of the course.
Algebra is the branch of mathematics which works with symbolic expressions and variables, and not just calculations with numbers.
Algebra is needed in many situations. For example algebra can be used to describe mathematical problems and to solve equations. Among other things it can describe geometric facts by means of algebraic statements, and many problems can be resolved with the help of algebraic operations.
In some cases the value of an expression does not simplify to a numeric value. The reason may be that the expression includes unknown parameters or variables. It may also be that it is important that a number be exactly specified, such as that given circle is to have a circumference of exactly \displaystyle 4\pi units, or the hypotenuse of a triangle is to b e\displaystyle \sqrt{3}, or even that the value of a constant is to be \displaystyle \dfrac{1-\ln 2}{3}.
Then it may be easier just to call the number, for example, a. In return, you must accept that you may not arrive at a numerical value, but instead may finish up with an expression that contains a.
A common situation where it algebra may be necessary is simplification. It is often very important to simplify an expression, such as before differentiation, or when an equation is to be solved.
Simplification reduces the risk of careless mistakes and avoids unnecessary work. To simplify means to transform an expression from one form to another. Which of these are considered as ”simple”is sometimes obvious, but it can also depend on what you want to do with the expression.
When differentiating, it may be advantageous to transform the expression into a sum of a number of terms. On the other hand when we solve an equation, it may be advantageous to reformulate the expression as a product of a number of factors. Therefore, one needs to be proficient in converting expressions into different forms.
It is important to note that the material in this section— as well as in other parts of the course — is designed that one does not use calculators.
When you get to university, you will not be allowed to use calculators during your "exams" at least this is true for the basic courses.
To succeed you with Algebra
- Start by reading the section's theory and study the examples.
- Work through the practice questions and try to solve them without using a calculator. Make sure that you have the right answer by clicking on the answer button. If you do not have it, you can click on the solution button to see what went wrong
- Then go ahead and answer the questions in the basic test of the section.
- If you get stuck on a point, check to see if someone else has discussed the point in the forum belonging to the section. If not, take up the point yourself. Your teacher (or a student) will respond to your question within a few hours.
- When you are finished with the exercises and the basic test in a section you should take the final test to get a pass for the section. The requirement here is to answer correctly three questions in a row before you can move on to the next section.
- When you have answered correctly all questions in both the basic and the final test of this section you will have a pass for this section and can move on to Part 3 of the course.
PS. If you feel that you are very familiar with the contents of a section you can test yourself by going directly to the basic and final tests. You must answer all the questions correctly in a test, but you may do the test several times if you do not succeed at the first attempt. It is your final results which appear in the statistics.