Lösung 4.4:5b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 7: | Zeile 7: | ||
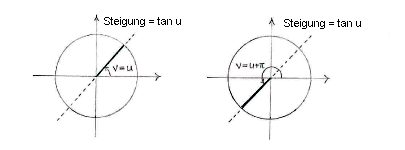
{{Abgesetzte Formel||<math>v=u\qquad\text{und}\qquad v=u+\pi\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>v=u\qquad\text{und}\qquad v=u+\pi\,\textrm{.}</math>}} | ||
| - | [[Image: | + | [[Image:4_4_5_b_de.gif|center]] |
Die allgemeine Lösung ist | Die allgemeine Lösung ist | ||
Version vom 15:52, 30. Jul. 2009
Wir betrachten zuerst die Gleichung
| \displaystyle \tan u=\tan v |
Diese Gleichung ist erfüllt, wenn
| \displaystyle v=u\qquad\text{und}\qquad v=u+\pi\,\textrm{.} |
Die allgemeine Lösung ist
| \displaystyle v=u+n\pi\,, |
Für unsere Gleichung
| \displaystyle \tan x=\tan 4x |
erhalten wir die Lösungen
| \displaystyle 4x = x+n\pi\,. |
Lösen wir diese Gleichung für x, erhalten wir
| \displaystyle x = \tfrac{1}{3}n\pi |