Lösung 4.4:1f
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
(Sprache und Formulierung) |
|||
| Zeile 6: | Zeile 6: | ||
| align="center" |[[Image:4_4_1_f-2.gif|center]] | | align="center" |[[Image:4_4_1_f-2.gif|center]] | ||
|- | |- | ||
| - | | align="center" |<small> | + | | align="center" |<small>Winkel 2π - π/6 = 11π/6</small> |
|| | || | ||
| - | | align="center" |<small> | + | | align="center" |<small>Winkel π + π/6 = 7π/6</small> |
|} | |} | ||
Die beiden Winkel, die <math>\sin v=-1/2</math> erfüllen liegen im dritten und vierten Quadranten, und sind <math>v=2\pi - \pi/6 = 11\pi/6</math> und <math>v = \pi + \pi/6 = 7\pi/6</math>. | Die beiden Winkel, die <math>\sin v=-1/2</math> erfüllen liegen im dritten und vierten Quadranten, und sind <math>v=2\pi - \pi/6 = 11\pi/6</math> und <math>v = \pi + \pi/6 = 7\pi/6</math>. | ||
Version vom 14:53, 27. Jul. 2009
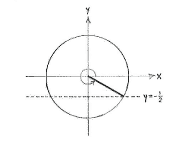
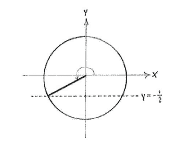
Wir suchen den Winkel, der der y-Koordinate \displaystyle -1/2 am Einheitskreis entspricht. Vergleichen wir diese Übung mit Übung a sehen wir, dass es dasselbe Problem ist, nur dass wir jetzt die Winkel suchen, die einen negativen Sinus haben.
| Winkel 2π - π/6 = 11π/6 | Winkel π + π/6 = 7π/6 |
Die beiden Winkel, die \displaystyle \sin v=-1/2 erfüllen liegen im dritten und vierten Quadranten, und sind \displaystyle v=2\pi - \pi/6 = 11\pi/6 und \displaystyle v = \pi + \pi/6 = 7\pi/6.