Lösung 2.2:6d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K |
||
| Zeile 1: | Zeile 1: | ||
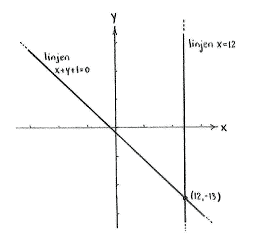
| - | Der Schnittpunkt muss beide Gleichungen der Geraden erfüllen | + | Der Schnittpunkt muss beide Gleichungen der Geraden erfüllen, also |
| - | {{Abgesetzte Formel||<math>x+y+1=0\qquad\text{ | + | {{Abgesetzte Formel||<math>x+y+1=0\qquad\text{und}\qquad x=12\,\textrm{.}</math>}} |
Wir substituieren <math>x=12</math> in der ersten Gleichung und erhalten | Wir substituieren <math>x=12</math> in der ersten Gleichung und erhalten | ||
Version vom 09:52, 9. Jun. 2009
Der Schnittpunkt muss beide Gleichungen der Geraden erfüllen, also
| \displaystyle x+y+1=0\qquad\text{und}\qquad x=12\,\textrm{.} |
Wir substituieren \displaystyle x=12 in der ersten Gleichung und erhalten
| \displaystyle 12+y+1=0\quad\Leftrightarrow\quad y=-13\,\textrm{,} |
Also ist der Schnittpunkt (12,-13).