Lösung 2.2:5c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Sprache und Formulierung)
Zeile 1: Zeile 1:
-
Zwei Geraden sind parallel, falls sie dieselbe Steigung haben. Wir sehen, dass die Gerade <math>y=3x+1</math> Steigung 3 hat, und also muss unsere Gerade die Gleichung
+
Zwei Geraden sind parallel, falls sie dieselbe Steigung haben. Wir sehen, dass die Gerade <math>y=3x+1</math> Steigung 3 hat, also muss unsere Gerade die Gleichung
{{Abgesetzte Formel||<math>y=3x+m\,,</math>}}
{{Abgesetzte Formel||<math>y=3x+m\,,</math>}}
-
haben, wo wir ''m'' bestimmen müssen. Nachdem die Gerade durch den Punkt (-1,2) gehen soll, muss dieser Punkt die Gleichung der Gerade erfüllen.
+
haben, wobei wir ''m'' bestimmen müssen. Nachdem die Gerade durch den Punkt (-1,2) gehen soll, muss dieser Punkt die Gleichung der Gerade erfüllen.
{{Abgesetzte Formel||<math>2=3\cdot (-1)+m\,,</math>}}
{{Abgesetzte Formel||<math>2=3\cdot (-1)+m\,,</math>}}
-
Dies ergibt <math>m=5</math>, und die Gleichung der Gerade ist daher <math>y=3x+5</math>.
+
Dies ergibt <math>m=5</math>, also ist die Gleichung der Gerade daher <math>y=3x+5</math>.
<center>[[Image:S1_2_2_5_c.jpg]]</center>
<center>[[Image:S1_2_2_5_c.jpg]]</center>

Version vom 09:21, 9. Aug. 2009

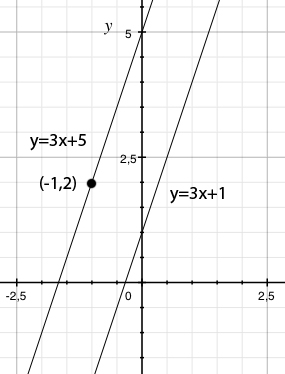
Zwei Geraden sind parallel, falls sie dieselbe Steigung haben. Wir sehen, dass die Gerade \displaystyle y=3x+1 Steigung 3 hat, also muss unsere Gerade die Gleichung

\displaystyle y=3x+m\,,

haben, wobei wir m bestimmen müssen. Nachdem die Gerade durch den Punkt (-1,2) gehen soll, muss dieser Punkt die Gleichung der Gerade erfüllen.

\displaystyle 2=3\cdot (-1)+m\,,

Dies ergibt \displaystyle m=5, also ist die Gleichung der Gerade daher \displaystyle y=3x+5.


Image:S1_2_2_5_c.jpg
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:5c“