Lösung 4.4:4

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Zeile 5: Zeile 5:
{{Abgesetzte Formel||<math>2v + 10^{\circ} = 110^{\circ}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>2v + 10^{\circ} = 110^{\circ}\,\textrm{.}</math>}}
-
Es gibt noch eine Lösung im Einheitskreis, nämlich im dritten Quadrant, mit denselben Winkel zur negativen ''y''-Achse, wie
+
Es gibt noch eine Lösung im Einheitskreis, nämlich im dritten Quadrant, mit denselben Winkel zur negativen ''y''-Achse, wie der Winkel <math>110^{\circ}</math> zur positiven ''y''-Achse hat, nur mit anderen Vorzeichen. Daher erhalten wir die zweite Lösung
-
There is then a further solution which satisfies <math>0^{\circ}\le 2v + 10^{\circ}\le 360^{\circ}</math>, where <math>2v+10^{\circ}</math> lies in the third quadrant and makes the same angle with the negative ''y''-axis as <math>100^{\circ}</math> makes with the positive ''y''-axis, i.e. <math>2v + 10^{\circ}</math> makes an angle <math>110^{\circ} - 90^{\circ} = 20^{\circ}</math>
+
-
with the negative ''y''-axis and consequently
+
{{Abgesetzte Formel||<math>2v + 10^{\circ} = 270^{\circ} - 20^{\circ} = 250^{\circ}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>2v + 10^{\circ} = 270^{\circ} - 20^{\circ} = 250^{\circ}\,\textrm{.}</math>}}
Zeile 13: Zeile 11:
[[Image:4_4_4.gif|center]]
[[Image:4_4_4.gif|center]]
-
Now it is easy to write down the general solution,
+
und die allgemeine Lösung ist
-
{{Abgesetzte Formel||<math>\left\{\begin{align} 2v + 10^{\circ} &= 110^{\circ} + n\cdot 360^{\circ}\quad\text{and}\\[5pt] 2v + 10^{\circ} &= 250^{\circ} + n\cdot 360^{\circ}\,,\end{align}\right.</math>}}
+
{{Abgesetzte Formel||<math>\left\{\begin{align} 2v + 10^{\circ} &= 110^{\circ} + n\cdot 360^{\circ}\quad\text{und}\\[5pt] 2v + 10^{\circ} &= 250^{\circ} + n\cdot 360^{\circ}\,,\end{align}\right.</math>}}
-
and if we make ''v'' the subject, we get
+
Lösen wir ''w'' erhalten wir
-
{{Abgesetzte Formel||<math>\left\{\begin{align} v &= 50^{\circ} + n\cdot 180^{\circ}\quad\text{and}\\[5pt] v &= 120^{\circ} + n\cdot 180^{\circ}\end{align}\right.</math>}}
+
{{Abgesetzte Formel||<math>\left\{\begin{align} v &= 50^{\circ} + n\cdot 180^{\circ}\quad\text{und}\\[5pt] v &= 120^{\circ} + n\cdot 180^{\circ}\end{align}\right.</math>}}
-
For different values of the integers ''n'', we see that the corresponding solutions are:
+
für verschiedene ''n'' erhalten wir unter anderen die Lösungen
Zeile 75: Zeile 73:
-
From the table, we see that the solutions that are between <math>0^{\circ}</math> and <math>360^{\circ}</math> are
+
Hieraus sehen wir die Lösungen die im Intervall von <math>0^{\circ}</math> bis <math>360^{\circ}</math> sind:
{{Abgesetzte Formel||<math>v = 50^{\circ},\quad v=120^{\circ },\quad v=230^{\circ}\quad\text{and}\quad v=300^{\circ}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>v = 50^{\circ},\quad v=120^{\circ },\quad v=230^{\circ}\quad\text{and}\quad v=300^{\circ}\,\textrm{.}</math>}}

Version vom 10:45, 7. Apr. 2009

Wir finden zuerst die allgemeine Lösung der Gleichung, und sehen danach welche der Winkeln im Intervall zwischen \displaystyle 0^{\circ} und \displaystyle 360^{\circ}\, liegen.

Wir betrachten zuerst den Ausdruck \displaystyle 2v+10^{\circ}, und erhalten die Lösung

\displaystyle 2v + 10^{\circ} = 110^{\circ}\,\textrm{.}

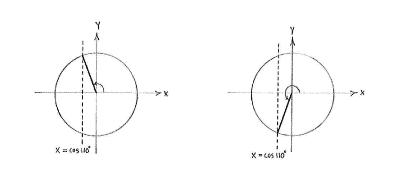
Es gibt noch eine Lösung im Einheitskreis, nämlich im dritten Quadrant, mit denselben Winkel zur negativen y-Achse, wie der Winkel \displaystyle 110^{\circ} zur positiven y-Achse hat, nur mit anderen Vorzeichen. Daher erhalten wir die zweite Lösung

\displaystyle 2v + 10^{\circ} = 270^{\circ} - 20^{\circ} = 250^{\circ}\,\textrm{.}

und die allgemeine Lösung ist

\displaystyle \left\{\begin{align} 2v + 10^{\circ} &= 110^{\circ} + n\cdot 360^{\circ}\quad\text{und}\\[5pt] 2v + 10^{\circ} &= 250^{\circ} + n\cdot 360^{\circ}\,,\end{align}\right.

Lösen wir w erhalten wir

\displaystyle \left\{\begin{align} v &= 50^{\circ} + n\cdot 180^{\circ}\quad\text{und}\\[5pt] v &= 120^{\circ} + n\cdot 180^{\circ}\end{align}\right.

für verschiedene n erhalten wir unter anderen die Lösungen


\displaystyle \cdots\cdots \displaystyle \cdots\cdots \displaystyle \cdots\cdots
\displaystyle n=-2:   \displaystyle v = 50^{\circ} - 2\cdot 180^{\circ} = -310^{\circ}   \displaystyle v = 120^{\circ } - 2\cdot 180^{\circ} = -240^{\circ}
\displaystyle n=-1: \displaystyle v = 50^{\circ} - 1\cdot 180^{\circ} = -130^{\circ} \displaystyle v = 120^{\circ} - 1\cdot 180^{\circ} = -60^{\circ}
\displaystyle n=0: \displaystyle v = 50^{\circ} + 0\cdot 180^{\circ} = 50^{\circ} \displaystyle v = 120^{\circ} + 0\cdot 180^{\circ} = 120^{\circ}
\displaystyle n=1: \displaystyle v = 50^{\circ} + 1\cdot 180^{\circ} = 230^{\circ} \displaystyle v = 120^{\circ} + 1\cdot 180^{\circ} = 300^{\circ}
\displaystyle n=2: \displaystyle v = 50^{\circ} + 2\cdot 180^{\circ} = 410^{\circ} \displaystyle v = 120^{\circ} + 2\cdot 180^{\circ} = 480^{\circ}
\displaystyle n=3: \displaystyle v = 50^{\circ} + 3\cdot 180^{\circ} = 590^{\circ} \displaystyle v = 120^{\circ} + 3\cdot 180^{\circ} = 660^{\circ}
\displaystyle \cdots\cdots \displaystyle \cdots\cdots \displaystyle \cdots\cdots


Hieraus sehen wir die Lösungen die im Intervall von \displaystyle 0^{\circ} bis \displaystyle 360^{\circ} sind:

\displaystyle v = 50^{\circ},\quad v=120^{\circ },\quad v=230^{\circ}\quad\text{and}\quad v=300^{\circ}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:4“