Lösung 4.3:9

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 3: Zeile 3:
{{Abgesetzte Formel||<math>\sin 160^{\circ} = 2\cos 80^{\circ}\sin 80^{\circ}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\sin 160^{\circ} = 2\cos 80^{\circ}\sin 80^{\circ}\,\textrm{.}</math>}}
-
Wir verwenden jetzt die Doppelwinkelfunktion für den Faktor <math>\sin 80^{\circ}</math>, nachdem wir den Faktor math>\cos 80^{\circ}</math> behalten möchten
+
Wir verwenden jetzt die Doppelwinkelfunktion für den Faktor <math>\sin 80^{\circ}</math>, nachdem wir den Faktor <math>\cos 80^{\circ}</math> behalten möchten:
-
{{Abgesetzte Formel||<math>2\cos 80^{\circ}\sin 80^{\circ} = 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\sin 40^{\circ}\,,</math>}}
+
{{Abgesetzte Formel||<math>2\cos 80^{\circ}\sin 80^{\circ} = 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\sin 40^{\circ}\,.</math>}}
Wir verwenden noch einmal die Doppelwinkelfunktion, dieses Mal für den Faktor <math>\sin 40^{\circ}</math>
Wir verwenden noch einmal die Doppelwinkelfunktion, dieses Mal für den Faktor <math>\sin 40^{\circ}</math>
Zeile 11: Zeile 11:
{{Abgesetzte Formel||<math>2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\cdot\sin 40^{\circ} = 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\cdot 2\cos 20^{\circ}\sin 20^{\circ}\,\textrm{·}</math>}}
{{Abgesetzte Formel||<math>2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\cdot\sin 40^{\circ} = 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\cdot 2\cos 20^{\circ}\sin 20^{\circ}\,\textrm{·}</math>}}
-
Also haben wir gezeigt dass
+
Also haben wir gezeigt, dass
{{Abgesetzte Formel||<math>\sin 160^{\circ} = 8\cos 80^{\circ}\cdot \cos 40^{\circ}\cdot \cos 20^{\circ}\cdot\sin 20^{\circ}</math>}}
{{Abgesetzte Formel||<math>\sin 160^{\circ} = 8\cos 80^{\circ}\cdot \cos 40^{\circ}\cdot \cos 20^{\circ}\cdot\sin 20^{\circ}</math>}}
-
oder anders geschrieben,
+
Anders geschrieben:
{{Abgesetzte Formel||<math>\cos 80^{\circ}\cdot\cos 40^{\circ}\cdot \cos 20^{\circ} = \frac{\sin 160^{\circ}}{8\sin 20^{\circ}}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\cos 80^{\circ}\cdot\cos 40^{\circ}\cdot \cos 20^{\circ} = \frac{\sin 160^{\circ}}{8\sin 20^{\circ}}\,\textrm{.}</math>}}
Zeile 21: Zeile 21:
[[Image:4_3_9.gif||right]]
[[Image:4_3_9.gif||right]]
-
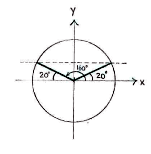
Zeichnen wir den Winkel <math>160^{\circ}</math> im Einheitskreis, sehen wir dass der Winkel denselben ''y''-Koordinaten wie der Winkel <math>20^{\circ}</math> hat, und daher denselben Sinus. Also erhalten wir
+
Zeichnen wir den Winkel <math>160^{\circ}</math> im Einheitskreis, sehen wir, dass der Winkel dieselbe ''y''-Koordinate wie der Winkel <math>20^{\circ}</math> hat und daher denselben Sinus. Also erhalten wir
<center><math>\sin 20^{\circ} = \sin 160^{\circ}\,\textrm{.}</math></center>
<center><math>\sin 20^{\circ} = \sin 160^{\circ}\,\textrm{.}</math></center>
-
und also haben wir die Gleichung
+
Damit haben wir die Gleichung
<center><math>\cos 80^{\circ} \cos 40^{\circ} \cos 20^{\circ} = \frac{\sin 160^{\circ}}{8\sin 20^{\circ}} = \frac{1}{8}\,\textrm{.}</math></center>
<center><math>\cos 80^{\circ} \cos 40^{\circ} \cos 20^{\circ} = \frac{\sin 160^{\circ}}{8\sin 20^{\circ}} = \frac{1}{8}\,\textrm{.}</math></center>
- 
-
gezeigt.
 

Version vom 13:10, 19. Jun. 2009

Wir verwenden die Doppelwinkelfunktion für \displaystyle \sin 160^{\circ}

\displaystyle \sin 160^{\circ} = 2\cos 80^{\circ}\sin 80^{\circ}\,\textrm{.}

Wir verwenden jetzt die Doppelwinkelfunktion für den Faktor \displaystyle \sin 80^{\circ}, nachdem wir den Faktor \displaystyle \cos 80^{\circ} behalten möchten:

\displaystyle 2\cos 80^{\circ}\sin 80^{\circ} = 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\sin 40^{\circ}\,.

Wir verwenden noch einmal die Doppelwinkelfunktion, dieses Mal für den Faktor \displaystyle \sin 40^{\circ}

\displaystyle 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\cdot\sin 40^{\circ} = 2\cos 80^{\circ}\cdot 2\cos 40^{\circ}\cdot 2\cos 20^{\circ}\sin 20^{\circ}\,\textrm{·}

Also haben wir gezeigt, dass

\displaystyle \sin 160^{\circ} = 8\cos 80^{\circ}\cdot \cos 40^{\circ}\cdot \cos 20^{\circ}\cdot\sin 20^{\circ}

Anders geschrieben:

\displaystyle \cos 80^{\circ}\cdot\cos 40^{\circ}\cdot \cos 20^{\circ} = \frac{\sin 160^{\circ}}{8\sin 20^{\circ}}\,\textrm{.}

Zeichnen wir den Winkel \displaystyle 160^{\circ} im Einheitskreis, sehen wir, dass der Winkel dieselbe y-Koordinate wie der Winkel \displaystyle 20^{\circ} hat und daher denselben Sinus. Also erhalten wir

\displaystyle \sin 20^{\circ} = \sin 160^{\circ}\,\textrm{.}

Damit haben wir die Gleichung

\displaystyle \cos 80^{\circ} \cos 40^{\circ} \cos 20^{\circ} = \frac{\sin 160^{\circ}}{8\sin 20^{\circ}} = \frac{1}{8}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:9“