Lösung 4.3:6b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Sprache und Formulierung)
Zeile 1: Zeile 1:
-
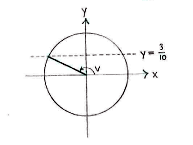
Wir zeichnen den Winkel <math>v</math> im Einheitskreis, mit der ''y''-Koordinate entsprechend <math>\sin v = 3/10</math>
+
Wir zeichnen den Winkel <math>v</math> auf den Einheitskreis, dessen ''y''-Koordinate <math>\sin v = 3/10</math> entspricht:
[[Image:4_3_6_b1.gif|center]]
[[Image:4_3_6_b1.gif|center]]
Zeile 7: Zeile 7:
[[Image:4_3_6_b2.gif|center]]
[[Image:4_3_6_b2.gif|center]]
-
Die Breite erhalten wir durch das Gesets des Pythagoras,
+
Die Breite erhalten wir durch das Gesetz des Pythagoras:
{{Abgesetzte Formel||<math>a^2 + \Bigl(\frac{3}{10}\Bigr)^2 = 1^2</math>}}
{{Abgesetzte Formel||<math>a^2 + \Bigl(\frac{3}{10}\Bigr)^2 = 1^2</math>}}
-
und wir erhalten
+
Wir erhalten:
{{Abgesetzte Formel||<math>a = \sqrt{1-\Bigl(\frac{3}{10}\Bigr)^2} = \sqrt{1-\frac{9}{100}} = \sqrt{\frac{91}{100}} = \frac{\sqrt{91}}{10}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>a = \sqrt{1-\Bigl(\frac{3}{10}\Bigr)^2} = \sqrt{1-\frac{9}{100}} = \sqrt{\frac{91}{100}} = \frac{\sqrt{91}}{10}\,\textrm{.}</math>}}
-
Also ist die ''x''Koordinate des Winkels <math>-a</math>, und wir erhalten
+
Also ist die ''x''Koordinate des Winkels <math>-a</math> und wir erhalten
{{Abgesetzte Formel||<math>\cos v=-\frac{\sqrt{91}}{10}</math>}}
{{Abgesetzte Formel||<math>\cos v=-\frac{\sqrt{91}}{10}</math>}}

Version vom 12:50, 19. Jun. 2009

Wir zeichnen den Winkel \displaystyle v auf den Einheitskreis, dessen y-Koordinate \displaystyle \sin v = 3/10 entspricht:

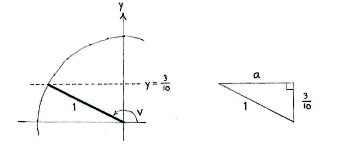
Wir zeichnen im zweiten Quadrant ein rechtwinkliges Dreieck mit der Hypotenuse 1 und der Höhe 3/10.

Die Breite erhalten wir durch das Gesetz des Pythagoras:

\displaystyle a^2 + \Bigl(\frac{3}{10}\Bigr)^2 = 1^2

Wir erhalten:

\displaystyle a = \sqrt{1-\Bigl(\frac{3}{10}\Bigr)^2} = \sqrt{1-\frac{9}{100}} = \sqrt{\frac{91}{100}} = \frac{\sqrt{91}}{10}\,\textrm{.}

Also ist die xKoordinate des Winkels \displaystyle -a und wir erhalten

\displaystyle \cos v=-\frac{\sqrt{91}}{10}

Also ist

\displaystyle \tan v = \frac{\sin v}{\cos v} = \frac{\dfrac{3}{10}}{-\dfrac{\sqrt{91}}{10}} = -\frac{3}{\sqrt{91}}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:6b“