Lösung 4.3:2a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Sprache und Formulierung)
Zeile 1: Zeile 1:
-
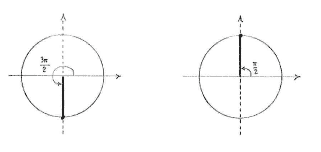
Am Einheitskreis entspricht der Winkel <math>3\pi/2</math> den Punkt (0,-1), und der Punkt zwischen <math>0</math> und <math>\pi</math> der denselben Kosinus wie <math>3\pi/2</math> hat, ist <math>v = \pi/2\,</math>, nachdem dieser Winkel am Einheitskreis auch die ''x''-Koordinate 0 hat.
+
Am Einheitskreis entspricht der Winkel <math>3\pi/2</math> dem Punkt (0,-1). Der Punkt zwischen <math>0</math> und <math>\pi</math> mit demselben Kosinus wie <math>3\pi/2</math> ist <math>v = \pi/2\,</math>, denn dieser Winkel hat am Einheitskreis auch die ''x''-Koordinate 0.
[[Image:4_3_2_a.gif||center]]
[[Image:4_3_2_a.gif||center]]

Version vom 09:12, 19. Jun. 2009

Am Einheitskreis entspricht der Winkel \displaystyle 3\pi/2 dem Punkt (0,-1). Der Punkt zwischen \displaystyle 0 und \displaystyle \pi mit demselben Kosinus wie \displaystyle 3\pi/2 ist \displaystyle v = \pi/2\,, denn dieser Winkel hat am Einheitskreis auch die x-Koordinate 0.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:2a“