Lösung 4.2:7

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
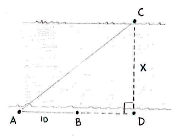
Wenn wir die Gerade AB zu einen Punkt D verlängern, der gegenüber von C liegt. bekommen wir ein rechtwinkliges Dreieck wie im unteren Bild, wo der Abstand ''x'' erfragt ist.
+
Wenn wir die Gerade AB zu einen Punkt D verlängern, der gegenüber von C liegt, bekommen wir ein rechtwinkliges Dreieck wie im unteren Bild, wobei der Abstand ''x'' der gesuchte Wert ist.
[[Image:4_2_7_1.gif|center]]
[[Image:4_2_7_1.gif|center]]
-
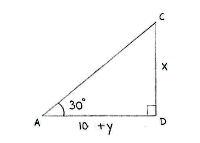
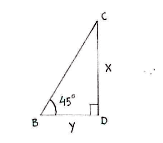
Wir betrachten die zwei Dreiecke ACD und BCD, und den Tangens für deren Winkeln 30° und 45°
+
Wir betrachten die zwei Dreiecke ACD und BCD und den Tangens für deren Winkeln 30° und 45°
{| align="center"
{| align="center"
Zeile 12: Zeile 12:
|align="center" valign="top"|<math>\begin{align} x &= (10+y)\tan 30^{\circ}\\[5pt] &= (10+y)\frac{1}{\sqrt{3}}\end{align}</math>
|align="center" valign="top"|<math>\begin{align} x &= (10+y)\tan 30^{\circ}\\[5pt] &= (10+y)\frac{1}{\sqrt{3}}\end{align}</math>
||
||
-
|align="center" valign="top"|<math>\begin{align} x &= y\cdot\tan 45^{\circ}\\[5pt] &= y\cdot 1\end{align}</math>
+
|align="center" valign="top"|<math>\begin{align} x &= y\cdot\tan 45^{\circ}\\[5pt] &= y\cdot 1\,.\end{align}</math>
|}
|}
-
,wo ''y'' der Abstand zwischen B und D ist.
+
''y'' seit der Abstand zwischen B und D.
-
Die zweite Gleichung gibt <math>y=x</math> und dies in der ersten Gleichung gibt
+
Die zweite Gleichung ergibt <math>y=x</math>. Dies in die erste Gleichung eingesetzt ergibt
{{Abgesetzte Formel||<math>x = (10+x)\frac{1}{\sqrt{3}}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x = (10+x)\frac{1}{\sqrt{3}}\,\textrm{.}</math>}}
-
Wir multiplizieren beide Seiten mit <math>\sqrt{3}</math>, und erhalten
+
Wir multiplizieren beide Seiten mit <math>\sqrt{3}</math> und erhalten
{{Abgesetzte Formel||<math>\sqrt{3}x=10+x</math>}}
{{Abgesetzte Formel||<math>\sqrt{3}x=10+x</math>}}
-
Wir sammeln alle ''x''-Terme auf einer Seite,
+
Wir schreiben alle ''x''-Terme auf einer Seite:
{{Abgesetzte Formel||<math>(\sqrt{3}-1)x = 10\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>(\sqrt{3}-1)x = 10\,\textrm{.}</math>}}
-
und also haben wir
+
Also haben wir
{{Abgesetzte Formel||<math>x = \frac{10}{\sqrt{3}-1}\ \text{m}\approx 13\textrm{.}6\ \text{m.}</math>}}
{{Abgesetzte Formel||<math>x = \frac{10}{\sqrt{3}-1}\ \text{m}\approx 13\textrm{.}6\ \text{m.}</math>}}

Version vom 13:29, 18. Jun. 2009

Wenn wir die Gerade AB zu einen Punkt D verlängern, der gegenüber von C liegt, bekommen wir ein rechtwinkliges Dreieck wie im unteren Bild, wobei der Abstand x der gesuchte Wert ist.

Wir betrachten die zwei Dreiecke ACD und BCD und den Tangens für deren Winkeln 30° und 45°

Image:4_2_7_2-1.gif   Image:4_2_7_2-2.gif
\displaystyle \begin{align} x &= (10+y)\tan 30^{\circ}\\[5pt] &= (10+y)\frac{1}{\sqrt{3}}\end{align} \displaystyle \begin{align} x &= y\cdot\tan 45^{\circ}\\[5pt] &= y\cdot 1\,.\end{align}

y seit der Abstand zwischen B und D.

Die zweite Gleichung ergibt \displaystyle y=x. Dies in die erste Gleichung eingesetzt ergibt

\displaystyle x = (10+x)\frac{1}{\sqrt{3}}\,\textrm{.}

Wir multiplizieren beide Seiten mit \displaystyle \sqrt{3} und erhalten

\displaystyle \sqrt{3}x=10+x

Wir schreiben alle x-Terme auf einer Seite:

\displaystyle (\sqrt{3}-1)x = 10\,\textrm{.}

Also haben wir

\displaystyle x = \frac{10}{\sqrt{3}-1}\ \text{m}\approx 13\textrm{.}6\ \text{m.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:7“