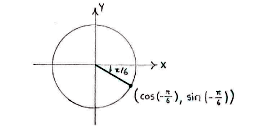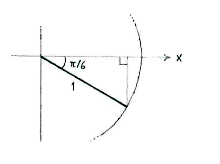Lösung 4.2:3f
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | Der Punkt auf den Einheitskreis der | + | Der Punkt auf den Einheitskreis, der dem Winkel <math>-\pi/6</math> entspricht, liegt im vierten Quadranten: |
[[Image:4_2_3_f1.gif||center]] | [[Image:4_2_3_f1.gif||center]] | ||
| - | Wir betrachten ein Dreieck im vierten | + | Wir betrachten ein Dreieck im vierten Quadranten: |
[[Image:4_2_3_f2.gif||center]] | [[Image:4_2_3_f2.gif||center]] | ||
| - | Wir berechnen zuerst die Katheten des Dreieckes | + | Wir berechnen zuerst die Katheten des Dreieckes und danach die Koordinaten des Punktes. |
{| width="100%" | {| width="100%" | ||
| Zeile 14: | Zeile 14: | ||
|} | |} | ||
| - | Die Koordinaten des Punktes auf den Einheitskreis | + | Die Koordinaten des Punktes auf den Einheitskreis entsprechen dem Winkel <math>-\pi/6</math> und sind also <math>(\sqrt{3}/2,-1/2)</math>. Inbesondere ist <math>\cos (-\pi/6) = \sqrt{3}/2\,</math>. |
Version vom 10:33, 18. Jun. 2009
Der Punkt auf den Einheitskreis, der dem Winkel \displaystyle -\pi/6 entspricht, liegt im vierten Quadranten:
Wir betrachten ein Dreieck im vierten Quadranten:
Wir berechnen zuerst die Katheten des Dreieckes und danach die Koordinaten des Punktes.
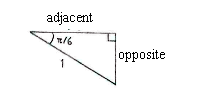
| \displaystyle \begin{align}\text{Gegenkathete} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{Ankathete} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align} |
Die Koordinaten des Punktes auf den Einheitskreis entsprechen dem Winkel \displaystyle -\pi/6 und sind also \displaystyle (\sqrt{3}/2,-1/2). Inbesondere ist \displaystyle \cos (-\pi/6) = \sqrt{3}/2\,.