Lösung 4.2:3b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
| Zeile 1: | Zeile 1: | ||
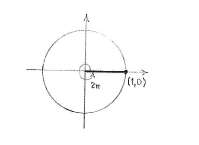
| - | Der Winkel <math>2\pi</math> entspricht einen ganzen Kreis, und also ist die Gerade mit dem Winkel <math>2\pi</math> zur ''x''-Achse die ''x''-Achse. | + | Der Winkel <math>2\pi</math> entspricht einen ganzen Kreis, und also ist die Gerade mit dem Winkel <math>2\pi</math> zur ''x''-Achse auch die ''x''-Achse. |
[[Image:4_2_3_b.gif|center]] | [[Image:4_2_3_b.gif|center]] | ||
Nachdem <math>\cos 2\pi</math> der ''x''-Koordinate der Schnittstelle von dieser Gerade und des Einheitskreises ist, sehen wir direkt dass <math>\cos 2\pi = 1\,</math>. | Nachdem <math>\cos 2\pi</math> der ''x''-Koordinate der Schnittstelle von dieser Gerade und des Einheitskreises ist, sehen wir direkt dass <math>\cos 2\pi = 1\,</math>. | ||
Version vom 12:24, 4. Apr. 2009
Der Winkel \displaystyle 2\pi entspricht einen ganzen Kreis, und also ist die Gerade mit dem Winkel \displaystyle 2\pi zur x-Achse auch die x-Achse.
Nachdem \displaystyle \cos 2\pi der x-Koordinate der Schnittstelle von dieser Gerade und des Einheitskreises ist, sehen wir direkt dass \displaystyle \cos 2\pi = 1\,.