Lösung 4.2:3a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
(Sprache und Formulierung) |
|||
| Zeile 1: | Zeile 1: | ||
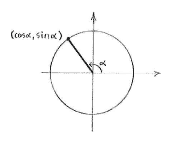
| - | Nachdem die trigonometrischen Funktionen von Winkeln die nicht zwischen <math>0</math> und <math>{\pi }/{2}\;</math> liegen durch den Einheitskreis definiert sind, verwenden wir | + | Nachdem die trigonometrischen Funktionen von Winkeln, die nicht zwischen <math>0</math> und <math>{\pi }/{2}\;</math> liegen, durch den Einheitskreis definiert sind, verwenden wir diesen: der Punkt auf dem Einheitskreis, der den Winkel <math>\alpha</math> zur ''x''-Achse bildet, hat die ''x''-Koordinaten, die <math>\cos \alpha</math> entspricht und eine ''y''-Koordinate, die <math>\sin \alpha</math> entspricht. |
[[Image:4_2_3_a1.gif|center]] | [[Image:4_2_3_a1.gif|center]] | ||
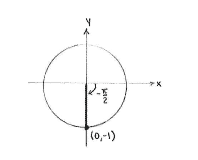
| - | In unseren Fall sehen wir direkt dass <math>\sin\Bigl(-\frac{\pi}{2}\Bigr) = -1\,</math>. | + | In unseren Fall sehen wir direkt, dass <math>\sin\Bigl(-\frac{\pi}{2}\Bigr) = -1\,</math>. |
[[Image:4_2_3_a2.gif|center]] | [[Image:4_2_3_a2.gif|center]] | ||
Version vom 10:10, 18. Jun. 2009
Nachdem die trigonometrischen Funktionen von Winkeln, die nicht zwischen \displaystyle 0 und \displaystyle {\pi }/{2}\; liegen, durch den Einheitskreis definiert sind, verwenden wir diesen: der Punkt auf dem Einheitskreis, der den Winkel \displaystyle \alpha zur x-Achse bildet, hat die x-Koordinaten, die \displaystyle \cos \alpha entspricht und eine y-Koordinate, die \displaystyle \sin \alpha entspricht.
In unseren Fall sehen wir direkt, dass \displaystyle \sin\Bigl(-\frac{\pi}{2}\Bigr) = -1\,.