Lösung 2.3:10c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Zeile 7: Zeile 7:
|align="center"|[[Image:2_3_10_c1-2.gif|center]]
|align="center"|[[Image:2_3_10_c1-2.gif|center]]
|-
|-
-
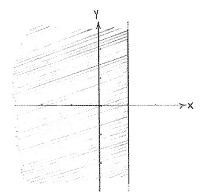
|align="center"|<small>The region 1&nbsp;≥&nbsp;''x''</small>
+
|align="center"|<small>Das Gebiet 1&nbsp;≥&nbsp;''x''</small>
||
||
-
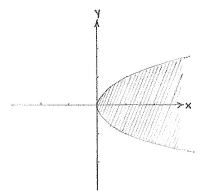
|align="center"|<small>The region ''x''&nbsp;≥&nbsp;''y''²</small>
+
|align="center"|<small>Das Gebiet ''x''&nbsp;≥&nbsp;''y''²</small>
|}
|}
Zeile 18: Zeile 18:
|align="center"|[[Image:2_3_10_c2.gif|center]]
|align="center"|[[Image:2_3_10_c2.gif|center]]
|-
|-
-
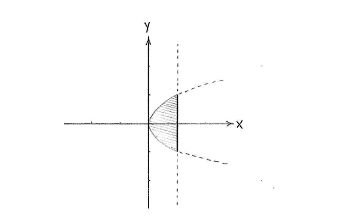
|align="center"|<small>The region 1&nbsp;≥&nbsp;''x''&nbsp;≥&nbsp;''y''²</small>
+
|align="center"|<small>Das Gebiet 1&nbsp;≥&nbsp;''x''&nbsp;≥&nbsp;''y''²</small>
|}
|}

Version vom 21:13, 16. Mär. 2009

Die Ungleichung \displaystyle 1\ge x\ge y^{2} definiert das Gebiet das die beiden Ungleichungen \displaystyle 1\ge x und \displaystyle x\ge y^{2} erfüllt. Die erste Ungleichung gibt dass unser Gebiet links von der Geaden \displaystyle x=1 sein muss. Die andere Ungleichung ist genau wie die Ungleichung \displaystyle y\ge x^{2}, nur haben x und y Platz getauscht. Daher drehen wir die Parabel \displaystyle y=x^{2} sodass sie entlang der x-Achse wächst.


 
Das Gebiet 1 ≥ x Das Gebiet x ≥ y²

Also bekommen wir das Gebiet zwischen der Parabel und der Gerade.


Das Gebiet 1 ≥ x ≥ y²
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:10c“