Lösung 2.2:6a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Sprache und Formulierung)
Zeile 1: Zeile 1:
-
Laut Definition ist der Schnittpunkt von zwei Geraden kreuzen, der Punkt der auf beiden Geraden liegt, und also muss der punkt die Gleichung beider Geraden erfüllen.
+
Laut Definition ist der Schnittpunkt zweier Geraden derjenige, welcher auf beiden Geraden liegt, also die Gleichungen beider Geraden erfüllt.
Wir benennen den Schnittpunkt (''x'',''y''),
Wir benennen den Schnittpunkt (''x'',''y''),
Zeile 6: Zeile 6:
<math>\left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.</math>}}
<math>\left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.</math>}}
-
<math>y=0</math> in der ersten Gleichung ersetzt, ergibt
+
<math>y=0</math> in die erste Gleichung eingesetzt ergibt
{{Abgesetzte Formel||<math>0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}</math>}}

Version vom 09:49, 9. Jun. 2009

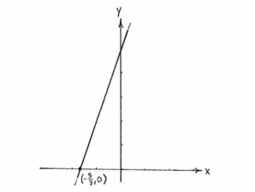
Laut Definition ist der Schnittpunkt zweier Geraden derjenige, welcher auf beiden Geraden liegt, also die Gleichungen beider Geraden erfüllt.

Wir benennen den Schnittpunkt (x,y),

\displaystyle \left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.

\displaystyle y=0 in die erste Gleichung eingesetzt ergibt

\displaystyle 0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}

Der Schnittpunkt der Geraden ist also (-5/3,0).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:6a“