Aus Online Mathematik Brückenkurs 1

Version vom 11:12, 13. Mär. 2009 (bearbeiten) Martin (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 09:41, 9. Jun. 2009 (bearbeiten) (rückgängig) Markus.bez (Diskussion | Beiträge) (Sprache und Formulierung) Zum nächsten Versionsunterschied →
Zeile 3:		Zeile 3:
	{{Abgesetzte Formel||<math>k_{2} = -\frac{1}{k_{1}} = -\frac{1}{2}</math>}}		{{Abgesetzte Formel||<math>k_{2} = -\frac{1}{k_{1}} = -\frac{1}{2}</math>}}
-	Nachdem die Gerade <math>y=2x+5</math> die Steigung <math>k_{1}=2</math> hat.	+	Also hat die Gerade <math>y=2x+5</math> die Steigung <math>k_{1}=2</math>.
	Also ist die Gleichung unserer Gerade		Also ist die Gleichung unserer Gerade

---

Version vom 09:41, 9. Jun. 2009

Wenn zwei nicht-senkrechte Geraden winkelrecht sind, gilt für deren Steigungen \displaystyle k_{1} und \displaystyle k_{2}, dass \displaystyle k_{1}k_{2}=-1, und daher erhalten wir die Steigung von unser Geraden als

\displaystyle k_{2} = -\frac{1}{k_{1}} = -\frac{1}{2}

Also hat die Gerade \displaystyle y=2x+5 die Steigung \displaystyle k_{1}=2.

Also ist die Gleichung unserer Gerade

\displaystyle y=-\frac{1}{2}x+m

wo m noch bestimmt werden muss.

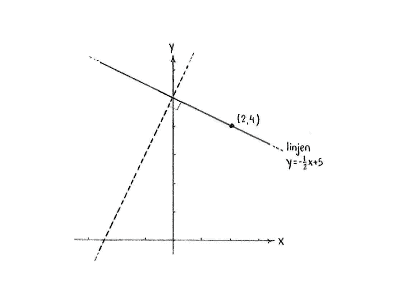
Nachdem der Punkt (2,4) auf der Gerade liegt, muss der Punkt (2,4) die Gleichung der Gerade erfüllen

\displaystyle 4=-\frac{1}{2}\cdot 2+m\,,

Also ist \displaystyle m=5. Die Gleichung der Gerade ist daher \displaystyle y=-\frac{1}{2}x+5.