Lösung 4.4:3c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.4:3c“ nach „Lösung 4.4:3c“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
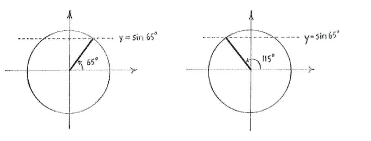
If we consider the entire expression <math>x + 40^{\circ}</math> as an unknown, we have a basic trigonometric equation and can, with the aid of the unit circle, see that there are two solutions to the equation for <math>0^{\circ}\le x+40^{\circ}\le 360^{\circ}</math> namely <math>x+40^{\circ} = 65^{\circ}</math> and the symmetric solution <math>x + 40^{\circ} = 180^{\circ} - 65^{\circ} = 115^{\circ}\,</math>.
+
Falls wir <math>x + 40^{\circ}</math> als unbekannter Variabel betrachten, haben wir eine einfache trigonometrische Gleichung wie vorher. Wir sehen dass es im Intervall <math>0^{\circ}\le x+40^{\circ}\le 360^{\circ}</math> zwei Lösungen gibt, nämlich <math>x+40^{\circ} = 65^{\circ}</math> und die symmetrische Lösung <math>x + 40^{\circ} = 180^{\circ} - 65^{\circ} = 115^{\circ}\,</math>.
[[Image:4_4_3_c.gif|center]]
[[Image:4_4_3_c.gif|center]]
-
It is then easy to set up the general solution by adding multiples of <math>360^{\circ}\,</math>,
+
Und die allgemeine Lösung ist
-
{{Abgesetzte Formel||<math>x + 40^{\circ} = 65^{\circ} + n\cdot 360^{\circ}\qquad\text{and}\qquad x + 40^{\circ} = 115^{\circ} + n\cdot 360^{\circ}</math>}}
+
{{Abgesetzte Formel||<math>x + 40^{\circ} = 65^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad x + 40^{\circ} = 115^{\circ} + n\cdot 360^{\circ}</math>}}
-
for all integers ''n'', which gives
+
und also erhalten wir die Lösungen
-
{{Abgesetzte Formel||<math>x = 25^{\circ} + n\cdot 360^{\circ}\qquad\text{and}\qquad x=75^{\circ} + n\cdot 360^{\circ}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x = 25^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad x=75^{\circ} + n\cdot 360^{\circ}\,\textrm{.}</math>}}

Version vom 09:23, 7. Apr. 2009

Falls wir \displaystyle x + 40^{\circ} als unbekannter Variabel betrachten, haben wir eine einfache trigonometrische Gleichung wie vorher. Wir sehen dass es im Intervall \displaystyle 0^{\circ}\le x+40^{\circ}\le 360^{\circ} zwei Lösungen gibt, nämlich \displaystyle x+40^{\circ} = 65^{\circ} und die symmetrische Lösung \displaystyle x + 40^{\circ} = 180^{\circ} - 65^{\circ} = 115^{\circ}\,.

Und die allgemeine Lösung ist

\displaystyle x + 40^{\circ} = 65^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad x + 40^{\circ} = 115^{\circ} + n\cdot 360^{\circ}

und also erhalten wir die Lösungen

\displaystyle x = 25^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad x=75^{\circ} + n\cdot 360^{\circ}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:3c“