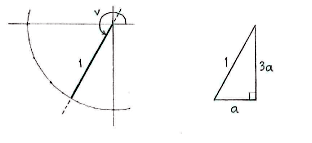Lösung 4.3:6c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.3:6c“ nach „Lösung 4.3:6c“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
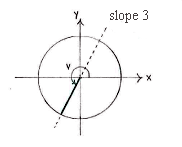
Because the angle <math>v</math> satisfies <math>\pi \le v\le 3\pi/2\,</math>, <math>v</math> belongs to the third quadrant in the unit circle. Furthermore, <math>\tan v = 3</math> gives that the line which corresponds to the angle
+
Nachdem der Winkel <math>\pi \le v\le 3\pi/2\,</math> erfüllt, liegt <math>v</math> im dritten Quadrant am Einheitskreis. Weiterhin ist <math>\tan v = 3</math>, und die Steigung der Geraden mit den Winkel <math>v</math> ist also 3.
-
<math>v</math> has slope 3.
+
[[Image:4_3_6_c1.gif|center]]
[[Image:4_3_6_c1.gif|center]]
-
In the third quadrant, we can introduce a right-angled triangle in which the hypotenuse is 1 and the sides have a 3:1 ratio.
+
Wir zeichnen ein Dreieck im dritten Quadrant, mit dem Verhältnis 3:1 zwischen Höhe und Breite.
[[Image:4_3_6_c2.gif|center]]
[[Image:4_3_6_c2.gif|center]]
-
If we now use the Pythagorean theorem on the triangle, we see that the horizontal side ''a'' satisfies
+
Auf Grund des Gesetz des Pythagoras erfüllt ''a'' die Gleichung
{{Abgesetzte Formel||<math>a^2 + (3a)^2 = 1^2</math>}}
{{Abgesetzte Formel||<math>a^2 + (3a)^2 = 1^2</math>}}
Zeile 14: Zeile 13:
which gives us that <math>10a^{2}=1</math> i.e. <math>a = 1/\!\sqrt{10}\,\textrm{.}</math>
which gives us that <math>10a^{2}=1</math> i.e. <math>a = 1/\!\sqrt{10}\,\textrm{.}</math>
-
Thus, the angle ''v'''s ''x''-coordinate is <math>-1/\!\sqrt{10}</math> and ''y''-coordinate is <math>-3/\!\sqrt{10}</math>, i.e.
+
Also ist di ''x'-Koordinate entsprechend den Winkel ''v'' <math>-1/\!\sqrt{10}</math> und die ''y''-Koordinate ist <math>-3/\!\sqrt{10}</math>. Also haben wir
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}

Version vom 13:05, 5. Apr. 2009

Nachdem der Winkel \displaystyle \pi \le v\le 3\pi/2\, erfüllt, liegt \displaystyle v im dritten Quadrant am Einheitskreis. Weiterhin ist \displaystyle \tan v = 3, und die Steigung der Geraden mit den Winkel \displaystyle v ist also 3.

Wir zeichnen ein Dreieck im dritten Quadrant, mit dem Verhältnis 3:1 zwischen Höhe und Breite.

Auf Grund des Gesetz des Pythagoras erfüllt a die Gleichung

\displaystyle a^2 + (3a)^2 = 1^2

which gives us that \displaystyle 10a^{2}=1 i.e. \displaystyle a = 1/\!\sqrt{10}\,\textrm{.}

Also ist di x'-Koordinate entsprechend den Winkel v \displaystyle -1/\!\sqrt{10} und die y-Koordinate ist \displaystyle -3/\!\sqrt{10}. Also haben wir

\displaystyle \begin{align}

\cos v &= -\frac{1}{\sqrt{10}}\,,\\[5pt] \sin v &= -\frac{3}{\sqrt{10}}\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:6c“