Lösung 4.3:1b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (hat „Solution 4.3:1b“ nach „Lösung 4.3:1b“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Nachdem der Sinus eines Winkels den ''y''-Koordinaten am Einheitskreis entspricht, gibt es zwei Winkeln am Einheitskreis mit denselben Sinus. Zeichnen wir <math>\pi/7</math> im Einheitskreis, sehen wir dass nur ein Winkel denselben ''y''-Wert hat, und noch dazu zwischen <math>\pi/2</math> und <math>\pi</math> liegt. | |
[[Image:4_3_1_b.gif||center]] | [[Image:4_3_1_b.gif||center]] | ||
| - | + | Auf Grund der Symmetrie der Spiegelung in der ''y''-Achse, ist dieser Winkel <math>v = \pi - \pi/7 = 6\pi/7\,</math>. | |
Version vom 11:27, 5. Apr. 2009
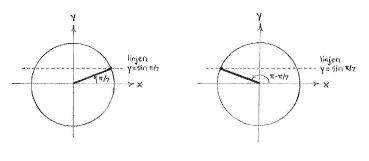
Nachdem der Sinus eines Winkels den y-Koordinaten am Einheitskreis entspricht, gibt es zwei Winkeln am Einheitskreis mit denselben Sinus. Zeichnen wir \displaystyle \pi/7 im Einheitskreis, sehen wir dass nur ein Winkel denselben y-Wert hat, und noch dazu zwischen \displaystyle \pi/2 und \displaystyle \pi liegt.
Auf Grund der Symmetrie der Spiegelung in der y-Achse, ist dieser Winkel \displaystyle v = \pi - \pi/7 = 6\pi/7\,.