Lösung 4.1:6c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.1:6c“ nach „Lösung 4.1:6c“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
What we need to do is to rewrite the equation in the standard form
+
Wir müssen die Gleichung des Kreises auf die Form
-
 
+
<math>\left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}</math>
<math>\left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}</math>
 +
bringen, wo wir direkt den Mittelpunkt <math>\left( a \right.,\left. b \right)</math> und den Radius <math>r</math> ablesen können.
-
because then we can read off the circle's centre
+
Wir bringen zuerst den Faktor <math>3</math> aus den Klammern heraus
-
<math>\left( a \right.,\left. b \right)</math>
+
-
and radius,
+
-
<math>r</math>.
+
-
 
+
-
In our case, we need only take out the factor
+
-
<math>~\text{3}</math>
+
-
from the brackets on the left-hand side
+
-
 
+
<math>\begin{align}
<math>\begin{align}
Zeile 20: Zeile 12:
\end{align}</math>
\end{align}</math>
-
 
+
und dividieren danach beide Seiten mit 9, und erhalten so die Gleichung
-
and then divide both sides by
+
-
<math>\text{9}</math>
+
-
, so as to get the equation in the desired form:
+
-
 
+
<math>\left( x-\frac{1}{3} \right)^{2}+\left( y+\frac{7}{3} \right)^{2}=\frac{10}{9}</math>
<math>\left( x-\frac{1}{3} \right)^{2}+\left( y+\frac{7}{3} \right)^{2}=\frac{10}{9}</math>
-
Because the right-hand side can be written as
+
Nachdem die rechte Seite
<math>\left( \sqrt{\frac{10}{9}} \right)^{2}</math>
<math>\left( \sqrt{\frac{10}{9}} \right)^{2}</math>
-
and the term
+
ist, und der term
<math>\left( y+\frac{7}{3} \right)^{2}</math>
<math>\left( y+\frac{7}{3} \right)^{2}</math>
-
as
+
wie
<math></math>
<math></math>
 +
geschrieben werden kann, erhalten wir die Gleichung
 +
 +
<math>\left( y-\left( -\frac{7}{3} \right) \right)^{2}</math>
-
<math>\left( y-\left( -\frac{7}{3} \right) \right)^{2}</math>, the equation describes a circle with its centre at
+
Dies ist die Gleichung eines Kreises mit dem Mittelpunkt
<math>\left( \frac{1}{3} \right.,\left. -\frac{7}{3} \right)</math>
<math>\left( \frac{1}{3} \right.,\left. -\frac{7}{3} \right)</math>
-
and radius
+
und dem Radius
<math>\sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}</math>
<math>\sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}</math>

Version vom 18:09, 2. Apr. 2009

Wir müssen die Gleichung des Kreises auf die Form

\displaystyle \left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}

bringen, wo wir direkt den Mittelpunkt \displaystyle \left( a \right.,\left. b \right) und den Radius \displaystyle r ablesen können.

Wir bringen zuerst den Faktor \displaystyle 3 aus den Klammern heraus

\displaystyle \begin{align} & \left( 3x-1 \right)^{2}+\left( 3y+7 \right)^{2}=3^{2}\left( x-\frac{1}{3} \right)^{2}+3^{2}\left( y+\frac{7}{3} \right)^{2} \\ & =9\left( x-\frac{1}{3} \right)^{2}+9\left( y+\frac{7}{3} \right)^{2} \\ \end{align}

und dividieren danach beide Seiten mit 9, und erhalten so die Gleichung

\displaystyle \left( x-\frac{1}{3} \right)^{2}+\left( y+\frac{7}{3} \right)^{2}=\frac{10}{9}

Nachdem die rechte Seite \displaystyle \left( \sqrt{\frac{10}{9}} \right)^{2} ist, und der term \displaystyle \left( y+\frac{7}{3} \right)^{2} wie \displaystyle geschrieben werden kann, erhalten wir die Gleichung

\displaystyle \left( y-\left( -\frac{7}{3} \right) \right)^{2}

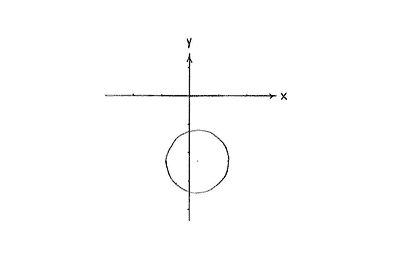
Dies ist die Gleichung eines Kreises mit dem Mittelpunkt \displaystyle \left( \frac{1}{3} \right.,\left. -\frac{7}{3} \right) und dem Radius \displaystyle \sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}

Image:4_1_6c-2(2).gif
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:6c“