Lösung 4.1:10

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.1:10“ nach „Lösung 4.1:10“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.
+
Zuerst schreiben wir alle Längen in dm (Dezimeter) sodass wir mit ganzen Zahlen arbeiten.
-
Call the length of the washing line from the trees to the hanger ''y'' and ''z'', as in the figure below, and introduce two auxiliary triangles which have ''y'' and ''z'' as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)
+
Wir benennen die Abstände von den Bäumen zum Kleidungstück ''y'' und ''z'', wie im Bild unten. Wir erhalten so zwei Dreiecke mit den Hypotenusen ''y'' und ''z'' (Wir haben angenommen dass das Kleidungsstück schwer ist, ond dass alle Abstände gerade sind).
<center> [[Image:4_1_10-1(5)_.gif]] </center>
<center> [[Image:4_1_10-1(5)_.gif]] </center>
-
 
+
Nachdem die Wäscheleine 54 dm lang ist erhalten wir
-
Because the line is 54 dm long, we have
+
{{Abgesetzte Formel||<math>y+z=54\,\textrm{.}</math>|(1)}}
{{Abgesetzte Formel||<math>y+z=54\,\textrm{.}</math>|(1)}}
-
Then, the Pythagorean theorem gives the relations
+
Mit dem Gesetz des Pythagoras erhalten wir
{{Abgesetzte Formel||<math>y^2 = x^2 + 12^2\,,</math>|(2)}}
{{Abgesetzte Formel||<math>y^2 = x^2 + 12^2\,,</math>|(2)}}
{{Abgesetzte Formel||<math>z^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3)}}
{{Abgesetzte Formel||<math>z^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3)}}
-
The idea now is to solve the system of equations (1)-(3) by first eliminating ''z'', so that we get two equations which only contain ''x'' and ''y''. Then, eliminate ''y'' from one of these equations, so that we get an equation which determines ''x''.
+
Wir lösen jetzt die Gleichungen (1)-(3), indem wir zuerst ''z'' eliminieren, und eine Gleichung mit nur ''x'' und ''y'' erhalten. Danach eliminieren wir ''y'', und erhalten so eine Gleichung mit nur ''x''.
-
From (1), we have <math>z = 54-y</math>, and substituting this into (3) gives us the equation
+
Von (1) erhalten wir <math>z = 54-y</math>, und dies in (3) ergibt
{{Abgesetzte Formel||<math>(54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3')}}
{{Abgesetzte Formel||<math>(54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}</math>|(3')}}
-
Equations (2) and (3') together give a smaller system for ''x'' and ''y'',
+
Jetzt haben wir nurmehr die Gleichungen (2) und (3), und die Unbekannten ''x'' und ''y'',
{{Abgesetzte Formel||<math>\left\{ \begin{align}
{{Abgesetzte Formel||<math>\left\{ \begin{align}
Zeile 29: Zeile 28:
\end{align} \right.</math>|<math>\begin{align}(2)\\[5pt] (3')\end{align}</math>}}
\end{align} \right.</math>|<math>\begin{align}(2)\\[5pt] (3')\end{align}</math>}}
-
Expand the quadratic terms on both sides of (3'),
+
Wir erweitern die Quadraten in (3'),
{{Abgesetzte Formel||<math>54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,</math>}}
{{Abgesetzte Formel||<math>54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,</math>}}
-
and simplify
+
und vereinfachen
{{Abgesetzte Formel||<math>2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}</math>}}
-
Use (2) and replace <math>y^2</math> with <math>x^2+12</math> in this equation,
+
Wir verwenden (2) und ersetzen <math>y^2</math> mit <math>x^2+12</math> in dieser Gleichung,
{{Abgesetzte Formel||<math>2916 - 108y + x^2 + 144 = x^2 + 12x + 1332</math>}}
{{Abgesetzte Formel||<math>2916 - 108y + x^2 + 144 = x^2 + 12x + 1332</math>}}
-
which gets rid of the ''x''²-term,
+
und so eliminieren wir alle''x''²-Terme,
{{Abgesetzte Formel||<math>2916 - 108y + 144 = 12x + 1332\,,</math>}}
{{Abgesetzte Formel||<math>2916 - 108y + 144 = 12x + 1332\,,</math>}}
-
and further simplification gives the equation
+
Durch weitere Vereinfachung erhalten wir
{{Abgesetzte Formel||<math>12x + 108y = 1728</math>|(3")}}
{{Abgesetzte Formel||<math>12x + 108y = 1728</math>|(3")}}
-
If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear
+
Wir haben jetzt die Gleichungen (2) und (3') in die Gleichungen (2) und (3'') gebracht, wo (3'') linear ist.
{{Abgesetzte Formel||<math>\left\{ \begin{align}
{{Abgesetzte Formel||<math>\left\{ \begin{align}
Zeile 56: Zeile 55:
\end{align} \right.</math>|<math>\begin{align}(2)\\[5pt] (3")\end{align}</math>}}
\end{align} \right.</math>|<math>\begin{align}(2)\\[5pt] (3")\end{align}</math>}}
-
In this system, we can make ''y'' the subject in (3"),
+
Wir lösen ''y'' in der Gleichung (3"),
{{Abgesetzte Formel||<math>y=\frac{1728-12x}{108}=16-\frac{x}{9}</math>}}
{{Abgesetzte Formel||<math>y=\frac{1728-12x}{108}=16-\frac{x}{9}</math>}}
-
and substitute into (2),
+
und ersetzen ''y'' mit <math>16-\frac{x}{9}</math> in (2),
{{Abgesetzte Formel||<math>\Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}</math>}}
-
This is an equation which only contains ''x'', and if we solve it, we will get our answer.
+
Dies ist eine Gleichung mit nur einen Unbekannten ''x'', und lösen wir diese Gleichung erhalten wir ''x''.
-
Expand the quadratic on the left-hand side,
+
Wir erweitern die Quadraten auf der linken Seite
{{Abgesetzte Formel||<math>16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144</math>}}
{{Abgesetzte Formel||<math>16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144</math>}}
-
and collect together all terms on one side,
+
und sammeln alle Terme auf einer Seite
{{Abgesetzte Formel||<math>x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,</math>}}
{{Abgesetzte Formel||<math>x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,</math>}}
-
which gives the equation
+
und erhalten so die Gleichung
{{Abgesetzte Formel||<math>\frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}</math>}}
-
Multiply both sides by <math>81/80</math> so that we get the equation in standard form,
+
Wir multiplizieren beide Seiten mit <math>81/80</math> sodass wir die Gleichung auf Standardform bringen,
{{Abgesetzte Formel||<math>x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}</math>}}
-
Completing the square on the left-hand side gives
+
Quadratische Ergänzung auf der linken Seite ergibt
{{Abgesetzte Formel||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0</math>}}
{{Abgesetzte Formel||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0</math>}}
-
and then
+
oder
{{Abgesetzte Formel||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,</math>}}
{{Abgesetzte Formel||<math>\Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,</math>}}
-
i.e.
+
und also ist
{{Abgesetzte Formel||<math>x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}</math>}}
-
This means that the equation has the solutions
+
Also hat die Gleichung die Lösungen
{{Abgesetzte Formel||<math>x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}</math>}}
-
The answer is thus <math>x=9\ \textrm{dm}</math> (the negative root must be discarded).
+
Die Antwort ist also <math>x=9\ \textrm{dm}</math> (Die Negative Lösung müssen wir verwerfen).
-
 
+
-
To be sure that we have calculated correctly, we also look at the values of ''y'' and ''z'', and check that the original equations (1) to (3) are satisfied.
+
Um zu prüfen ob wir richtig gerechnet haben, können wir zuerst ''y'' und ''z'' berechnen, und testen ob diese Werte zusammen mit ''x'' die Gleichungen (1) - (3) erfüllen.
-
Equation (3") gives
+
Die Gleichung (3") gibt
{{Abgesetzte Formel||<math>y = 16-\frac{x}{9} = 16-1 = 15</math>}}
{{Abgesetzte Formel||<math>y = 16-\frac{x}{9} = 16-1 = 15</math>}}
-
and equation (1) gives
+
und die Gleichung (1) gibt
{{Abgesetzte Formel||<math>z=54-y=54-15=39\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>z=54-y=54-15=39\,\textrm{.}</math>}}
-
Now, we check that <math>x=9</math>, <math>y=15</math> and <math>z=39</math> satisfy the equations (1), (2) and (3),
+
Jetzt prüfen wir ob <math>x=9</math>, <math>y=15</math> und <math>z=39</math> die Gleichungen (1), (2) und (3) erfüllen,
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
-
\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt]
+
\textrm{Linke Seite von (1)} &= 15+39 = 54\,,\\[5pt]
-
\textrm{RHS of (1)} &= 54\,,\\[10pt]
+
\textrm{Rechte Seite von (1)} &= 54\,,\\[10pt]
-
\textrm{LHS of (2)} &= 15^2 = 225\,,\\[5pt]
+
\textrm{Linke Seite von (2)} &= 15^2 = 225\,,\\[5pt]
-
\textrm{RHS of (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt]
+
\textrm{Rechte Seite von (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt]
-
\textrm{LHS of (3)} &= 39^2 = 1521\,,\\[5pt]
+
\textrm{Linke Seite von (3)} &= 39^2 = 1521\,,\\[5pt]
-
\textrm{RHS of (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.}
+
\textrm{Rechte Seite von (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}

Version vom 18:57, 2. Apr. 2009

Zuerst schreiben wir alle Längen in dm (Dezimeter) sodass wir mit ganzen Zahlen arbeiten.

Wir benennen die Abstände von den Bäumen zum Kleidungstück y und z, wie im Bild unten. Wir erhalten so zwei Dreiecke mit den Hypotenusen y und z (Wir haben angenommen dass das Kleidungsstück schwer ist, ond dass alle Abstände gerade sind).


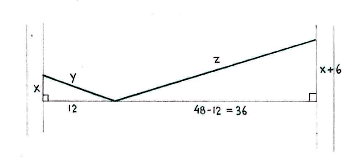
Image:4_1_10-1(5)_.gif

Nachdem die Wäscheleine 54 dm lang ist erhalten wir

\displaystyle y+z=54\,\textrm{.} (1)

Mit dem Gesetz des Pythagoras erhalten wir

\displaystyle y^2 = x^2 + 12^2\,, (2)
\displaystyle z^2 = (x+6)^2 + 36^2\,\textrm{.} (3)

Wir lösen jetzt die Gleichungen (1)-(3), indem wir zuerst z eliminieren, und eine Gleichung mit nur x und y erhalten. Danach eliminieren wir y, und erhalten so eine Gleichung mit nur x.

Von (1) erhalten wir \displaystyle z = 54-y, und dies in (3) ergibt

\displaystyle (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} (3')

Jetzt haben wir nurmehr die Gleichungen (2) und (3), und die Unbekannten x und y,

\displaystyle \left\{ \begin{align}

& y^2 = x^2 + 12^2\,,\\[5pt] & (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3')\end{align}

Wir erweitern die Quadraten in (3'),

\displaystyle 54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,

und vereinfachen

\displaystyle 2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}

Wir verwenden (2) und ersetzen \displaystyle y^2 mit \displaystyle x^2+12 in dieser Gleichung,

\displaystyle 2916 - 108y + x^2 + 144 = x^2 + 12x + 1332

und so eliminieren wir allex²-Terme,

\displaystyle 2916 - 108y + 144 = 12x + 1332\,,

Durch weitere Vereinfachung erhalten wir

\displaystyle 12x + 108y = 1728 (3")

Wir haben jetzt die Gleichungen (2) und (3') in die Gleichungen (2) und (3) gebracht, wo (3) linear ist.

\displaystyle \left\{ \begin{align}

& y^2 = x^2 + 12^2\,,\\[5pt] & 12x+108y=1728\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3")\end{align}

Wir lösen y in der Gleichung (3"),

\displaystyle y=\frac{1728-12x}{108}=16-\frac{x}{9}

und ersetzen y mit \displaystyle 16-\frac{x}{9} in (2),

\displaystyle \Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}

Dies ist eine Gleichung mit nur einen Unbekannten x, und lösen wir diese Gleichung erhalten wir x.

Wir erweitern die Quadraten auf der linken Seite

\displaystyle 16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144

und sammeln alle Terme auf einer Seite

\displaystyle x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,

und erhalten so die Gleichung

\displaystyle \frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}

Wir multiplizieren beide Seiten mit \displaystyle 81/80 sodass wir die Gleichung auf Standardform bringen,

\displaystyle x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}

Quadratische Ergänzung auf der linken Seite ergibt

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0

oder

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,

und also ist

\displaystyle x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}

Also hat die Gleichung die Lösungen

\displaystyle x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}

Die Antwort ist also \displaystyle x=9\ \textrm{dm} (Die Negative Lösung müssen wir verwerfen).

Um zu prüfen ob wir richtig gerechnet haben, können wir zuerst y und z berechnen, und testen ob diese Werte zusammen mit x die Gleichungen (1) - (3) erfüllen.

Die Gleichung (3") gibt

\displaystyle y = 16-\frac{x}{9} = 16-1 = 15

und die Gleichung (1) gibt

\displaystyle z=54-y=54-15=39\,\textrm{.}

Jetzt prüfen wir ob \displaystyle x=9, \displaystyle y=15 und \displaystyle z=39 die Gleichungen (1), (2) und (3) erfüllen,

\displaystyle \begin{align}

\textrm{Linke Seite von (1)} &= 15+39 = 54\,,\\[5pt] \textrm{Rechte Seite von (1)} &= 54\,,\\[10pt] \textrm{Linke Seite von (2)} &= 15^2 = 225\,,\\[5pt] \textrm{Rechte Seite von (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt] \textrm{Linke Seite von (3)} &= 39^2 = 1521\,,\\[5pt] \textrm{Rechte Seite von (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:10“