Lösung 2.3:10b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 2.3:10b“ nach „Lösung 2.3:10b“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
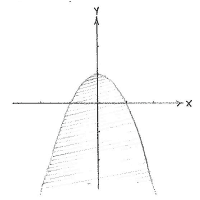
The inequality <math>y\le 1-x^{2}</math> defines the area under and on the curve
+
Die Ungleichung <math>y\le 1-x^{2}</math> definiert das Gebiet unter der Parabel
-
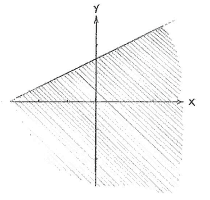
<math>y=1-x^{2}</math>, which is a parabola with a maximum at (0,1). We can rewrite the other inequality <math>x\ge 2y-3</math> as <math>y\le x/2+3/2</math> and it defines the area under and on the straight line <math>y=x/2+3/2</math>.
+
<math>y=1-x^{2}</math>. Die andere Ungleichung <math>x\ge 2y-3</math> können wir wie <math>y\le x/2+3/2</math> schreiben, und daher definiert sie das Gebiet Unter der Gerade <math>y=x/2+3/2</math>.
Zeile 13: Zeile 13:
|}
|}
-
 
+
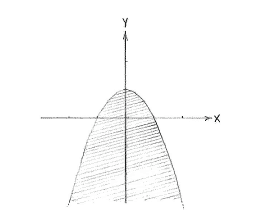
Es scheint so zu sein, als liegt die Gerade ganz oberhalb der Parabel. Dies würde bedeuten dass die Ungleichung <math>y\le 1-x^{2}</math> auch die Ungleichung <math>y\le x/2+3/2</math> erfüllt.
-
Of the figures above, it seems that the region associated with the parabola lies completely under the line <math>y=x/2+3/2</math> and this means that the area under the parabola satisfies both inequalities.
+
Zeile 23: Zeile 22:
|}
|}
-
 
+
Wir kontrollieren ob so auch der Fall ist, nämlich ob der ''y''-Wert der Gerade immer größer als der ''y''-Wert der Parabel für denselben ''x''-Wert ist. Wir betrachten den Unterschied
-
Note: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the ''y''-values on the line <math>y_{\scriptstyle\text{line}} = x/2+3/2</math> is always larger than the corresponding ''y''-value on the parabola <math>y_{\scriptstyle\text{parabola}} = 1-x^{2}</math> by studying the difference between them
+
{{Abgesetzte Formel||
{{Abgesetzte Formel||
<math>y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.}</math>}}
<math>y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.}</math>}}
-
If this difference is positive regardless of how ''x'' is chosen, then we know that the line's ''y''-value is always greater than the parabola's ''y''-value. After a little simplification and completing the square, we have
+
Durch ein wenig Vereinfachungen erhalten wir
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
-
y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}}
+
y_{\scriptstyle\text{Gerade}} - y_{\scriptstyle\text{Parabel}}
&= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt]
&= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt]
&= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt]
&= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt]
Zeile 39: Zeile 37:
\end{align}</math>}}
\end{align}</math>}}
-
and this expression is always positive because <math>\tfrac{7}{16}</math> is a positive number and <math>\bigl(x+\tfrac{1}{4}\bigr)^{2}</math> is a quadratic which is never negative. In other words, the parabola is completely under the line.
+
Wir sehen hier dass der Ausdruck immer positiv ist, nachdem <math>\tfrac{7}{16}</math> positiv ist, und <math>\bigl(x+\tfrac{1}{4}\bigr)^{2}</math> immer größer als, oder gleich null ist. Also liegt die Parabel ganz unterhalt der Gerade.

Version vom 21:02, 16. Mär. 2009

Die Ungleichung \displaystyle y\le 1-x^{2} definiert das Gebiet unter der Parabel \displaystyle y=1-x^{2}. Die andere Ungleichung \displaystyle x\ge 2y-3 können wir wie \displaystyle y\le x/2+3/2 schreiben, und daher definiert sie das Gebiet Unter der Gerade \displaystyle y=x/2+3/2.


 
The region y ≤ 1 - x² The region x ≥ 2y - 3

Es scheint so zu sein, als liegt die Gerade ganz oberhalb der Parabel. Dies würde bedeuten dass die Ungleichung \displaystyle y\le 1-x^{2} auch die Ungleichung \displaystyle y\le x/2+3/2 erfüllt.


The region y ≤ 1 - x² and x ≥ 2y - 3

Wir kontrollieren ob so auch der Fall ist, nämlich ob der y-Wert der Gerade immer größer als der y-Wert der Parabel für denselben x-Wert ist. Wir betrachten den Unterschied

\displaystyle y_{\scriptstyle\text{line}} - y_{\scriptstyle\text{parabola}} = \frac{x}{2} + \frac{3}{2} - (1-x^{2})\,\textrm{.}

Durch ein wenig Vereinfachungen erhalten wir

\displaystyle \begin{align}

y_{\scriptstyle\text{Gerade}} - y_{\scriptstyle\text{Parabel}} &= \frac{x}{2} + \frac{3}{2} - (1-x^{2})\\[5pt] &= x^{2}+\frac{1}{2}x+\frac{1}{2}\\[5pt] &= \Bigl(x+\frac{1}{4}\Bigr)^{2} - \Bigl(\frac{1}{4}\Bigr)^{2} + \frac{1}{2}\\[5pt] &= \Bigl(x+\frac{1}{4}\Bigr)^{2} + \frac{7}{16} \end{align}

Wir sehen hier dass der Ausdruck immer positiv ist, nachdem \displaystyle \tfrac{7}{16} positiv ist, und \displaystyle \bigl(x+\tfrac{1}{4}\bigr)^{2} immer größer als, oder gleich null ist. Also liegt die Parabel ganz unterhalt der Gerade.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:10b“