Lösung 2.2:6a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 2.2:6a“ nach „Lösung 2.2:6a“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
According to the definition, the point of intersection between two lines is that point which lies on both lines; it must therefore satisfy the equations of both lines.
+
Laut Definition ist der Schnittpunkt von zwei Geraden kreuzen, der Punkt der auf beiden Geraden liegt, und also muss der punkt die Gleichung beider Geraden erfüllen.
-
If the point of intersection has coordinates (''x'',''y''), then
+
Wir benennen den Schnittpunkt (''x'',''y''),
{{Abgesetzte Formel||
{{Abgesetzte Formel||
<math>\left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.</math>}}
<math>\left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.</math>}}
-
If we substitute <math>y=0</math> into the first equation, we obtain
+
<math>y=0</math> in der ersten Gleichung ersetzt, ergibt
{{Abgesetzte Formel||<math>0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}</math>}}
-
The point of intersection is (-5/3,0).
+
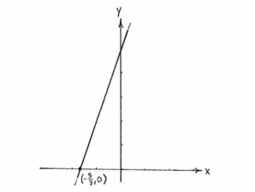
Der Schnittpunkt der Geraden ist also (-5/3,0).
<center>[[Image:2_2_6_a.gif|center]]</center>
<center>[[Image:2_2_6_a.gif|center]]</center>

Version vom 11:24, 13. Mär. 2009

Laut Definition ist der Schnittpunkt von zwei Geraden kreuzen, der Punkt der auf beiden Geraden liegt, und also muss der punkt die Gleichung beider Geraden erfüllen.

Wir benennen den Schnittpunkt (x,y),

\displaystyle \left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.

\displaystyle y=0 in der ersten Gleichung ersetzt, ergibt

\displaystyle 0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}

Der Schnittpunkt der Geraden ist also (-5/3,0).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:6a“