Lösung 2.2:5d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (hat „Solution 2.2:5d“ nach „Lösung 2.2:5d“ verschoben: Robot: moved page) |
Version vom 13:58, 22. Okt. 2008
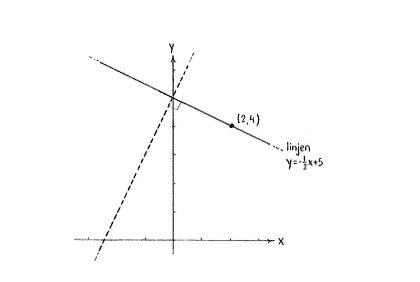
If two non-vertical lines are perpendicular to each other, their slopes \displaystyle k_{1} and \displaystyle k_{2} satisfy the relation \displaystyle k_{1}k_{2}=-1, and from this we have that the line we are looking for must have a slope that is given by
| \displaystyle k_{2} = -\frac{1}{k_{1}} = -\frac{1}{2} |
since the line \displaystyle y=2x+5 has a slope \displaystyle k_{1}=2 (the coefficient in front of x).
The line we are looking for can thus be written in the form
| \displaystyle y=-\frac{1}{2}x+m |
with m as an unknown constant.
Because the point (2,4) should lie on the line, (2,4) must satisfy the equation of the line,
| \displaystyle 4=-\frac{1}{2}\cdot 2+m\,, |
i.e. \displaystyle m=5. The equation of the line is \displaystyle y=-\frac{1}{2}x+5.