Lösung 4.3:5
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 12: | Zeile 12: | ||
Then, using the definition of cosine and tangent, | Then, using the definition of cosine and tangent, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
\cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt] | \cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt] | ||
\tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.} | \tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.} | ||
Version vom 08:55, 22. Okt. 2008
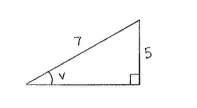
An often-used technique to calculate \displaystyle \cos v and \displaystyle \tan v, given the sine value of an acute angle, is to draw the angle \displaystyle v in a right-angled triangle which has two sides arranged so that \displaystyle \sin v = 5/7\,.
Using the Pythagorean theorem, we can determine the length of the third side in the triangle.
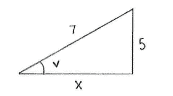
| \displaystyle \begin{align}&x^2 + 5^2 = 7^2\\[5pt] &\text{which gives that}\\[5pt] &x = \sqrt{7^2-5^2} = \sqrt{24} = 2\sqrt{6}\end{align} |
Then, using the definition of cosine and tangent,
| \displaystyle \begin{align}
\cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt] \tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.} \end{align} |
Note: The right-angled triangle that we use is just a tool and has nothing to do with the triangle that is referred to in the question.