Lösung 4.1:9
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
10 seconds corresponds to 1/6 minutes, so that during that time period, the second hand sweeps over 1/6 of a turn, i.e. the sector of a circle with angle | 10 seconds corresponds to 1/6 minutes, so that during that time period, the second hand sweeps over 1/6 of a turn, i.e. the sector of a circle with angle | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\alpha = \frac{1}{6}\cdot 2\pi\ \text{radians} = \frac{\pi}{3}\ \text{radians.}</math>}} |
<center> [[Image:4_1_9_.gif]] </center> | <center> [[Image:4_1_9_.gif]] </center> | ||
| Zeile 7: | Zeile 7: | ||
The area of the sector is | The area of the sector is | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\text{Area} = \frac{1}{2}\alpha r^{2} = \frac{1}{2}\cdot \frac{\pi}{3}\cdot (8\ \text{cm})^2 = \frac{32\pi}{3}\ \text{cm}^{2} \approx 33\textrm{.}5\ \text{cm}^{2}\,\textrm{.}</math>}} |
Version vom 08:49, 22. Okt. 2008
10 seconds corresponds to 1/6 minutes, so that during that time period, the second hand sweeps over 1/6 of a turn, i.e. the sector of a circle with angle
| \displaystyle \alpha = \frac{1}{6}\cdot 2\pi\ \text{radians} = \frac{\pi}{3}\ \text{radians.} |
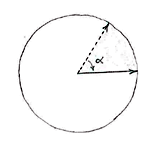
The area of the sector is
| \displaystyle \text{Area} = \frac{1}{2}\alpha r^{2} = \frac{1}{2}\cdot \frac{\pi}{3}\cdot (8\ \text{cm})^2 = \frac{32\pi}{3}\ \text{cm}^{2} \approx 33\textrm{.}5\ \text{cm}^{2}\,\textrm{.} |
