Lösung 4.4:5a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
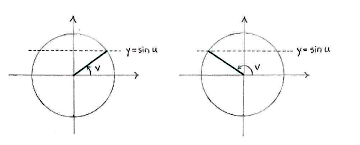
If we consider for a moment the equality | If we consider for a moment the equality | ||
| + | {{Displayed math||<math>\sin u = \sin v</math>|(*)}} | ||
| - | + | where ''u'' has a fixed value, there are usually two angles ''v'' in the unit circle which ensure that the equality holds, | |
| + | {{Displayed math||<math>v=u\qquad\text{and}\qquad v=\pi-u\,\textrm{.}</math>}} | ||
| + | [[Image:4_4_5_a.gif||center]] | ||
| - | + | (The only exception is when <math>u = \pi/2</math> or <math>u=3\pi/2</math>, in which case <math>u</math> and <math>\pi-u</math> correspond to the same direction and there is only one angle ''v'' which satisfies the equality.) | |
| - | <math>u</math> | + | |
| - | + | ||
| - | <math> | + | |
| - | in the | + | |
| + | We obtain all the angles ''v'' which satisfy (*) by adding multiples of <math>2\pi</math>, | ||
| - | <math>v=u | + | {{Displayed math||<math>v = u+2n\pi\qquad\text{and}\qquad v = \pi-u+2n\pi\,,</math>}} |
| - | and | + | |
| - | + | ||
| - | + | where ''n'' is an arbitrary integer. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | where | + | |
| - | + | ||
| - | is an arbitrary integer. | + | |
If we now go back to our equation | If we now go back to our equation | ||
| + | {{Displayed math||<math>\sin 3x = \sin x</math>}} | ||
| - | + | the reasoning above shows that the equation is only satisfied when | |
| - | + | ||
| - | + | ||
| - | the reasoning above shows | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | {{Displayed math||<math>3x = x+2n\pi\qquad\text{or}\qquad 3x = \pi-x+2n\pi\,\textrm{.}</math>}} | |
| - | <math>x</math> | + | |
| - | + | ||
| + | If we make ''x'' the subject of each equation, we obtain the full solution to the equation, | ||
| - | <math>\left\{ \begin{ | + | {{Displayed math||<math>\left\{\begin{align} |
| - | x=0+n\pi | + | x &= 0+n\pi\,,\\[5pt] |
| - | x=\frac{\pi }{4}+\frac{ | + | x &= \frac{\pi}{4}+\frac{n\pi}{2}\,\textrm{.} |
| - | \end{ | + | \end{align}\right.</math>}} |
Version vom 13:53, 13. Okt. 2008
If we consider for a moment the equality
where u has a fixed value, there are usually two angles v in the unit circle which ensure that the equality holds,
(The only exception is when \displaystyle u = \pi/2 or \displaystyle u=3\pi/2, in which case \displaystyle u and \displaystyle \pi-u correspond to the same direction and there is only one angle v which satisfies the equality.)
We obtain all the angles v which satisfy (*) by adding multiples of \displaystyle 2\pi,
where n is an arbitrary integer.
If we now go back to our equation
the reasoning above shows that the equation is only satisfied when
If we make x the subject of each equation, we obtain the full solution to the equation,