Lösung 4.4:2c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
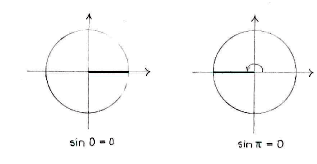
There are two angles in the unit circle,
+
There are two angles in the unit circle, <math>x=0</math> and <math>x=\pi</math>, whose sine has a value of zero.
-
<math>x=0\text{ }</math>
+
-
and
+
-
<math>x=\pi </math>, whose sine has a value of zero.
+
[[Image:4_4_2_c.gif|center]]
[[Image:4_4_2_c.gif|center]]
-
We get the full solution when we add multiples of
+
We get the full solution when we add multiples of <math>2\pi</math>,
-
<math>2\pi </math>,
+
 +
{{Displayed math||<math>x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,,</math>}}
-
<math>x=0+2n\pi </math>
+
where ''n'' is an arbitrary integer.
-
and
+
-
<math>x=\pi +2n\pi </math>,
+
-
where
 
-
<math>n</math>
 
-
is an arbitrary integer.
 
-
NOTE: Because the difference between
+
Note: Because the difference between <math>0</math> and <math>\pi</math> is a half turn, the solutions are repeated every half turn and they can be summarized in one expression,
-
<math>0</math>
+
-
and
+
-
<math>\pi </math>
+
-
is a half turn, the solutions are repeated every half turn and they can be summarized in one expression:
+
 +
{{Displayed math||<math>x=0+n\pi\,,</math>}}
-
<math>x=0+n\pi </math>
+
where ''n'' is an arbitrary integer.
-
 
+
-
 
+
-
where
+
-
<math>n</math>
+
-
is an arbitrary integer.
+

Version vom 14:25, 10. Okt. 2008

There are two angles in the unit circle, \displaystyle x=0 and \displaystyle x=\pi, whose sine has a value of zero.

We get the full solution when we add multiples of \displaystyle 2\pi,

Vorlage:Displayed math

where n is an arbitrary integer.


Note: Because the difference between \displaystyle 0 and \displaystyle \pi is a half turn, the solutions are repeated every half turn and they can be summarized in one expression,

Vorlage:Displayed math

where n is an arbitrary integer.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:2c“