Lösung 4.4:1b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
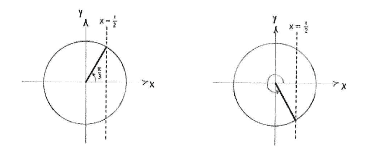
The easiest angle to find is
+
The easiest angle to find is <math>v = \pi/3</math> in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive ''x''-axis as <math>v=\pi/3</math>, but is under the ''x''-axis, also has a cosine value of 1/2 (same ''x''-coordinate).
-
<math>v={\pi }/{3}\;</math>
+
-
in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive
+
-
<math>x</math>
+
-
-axis as
+
-
<math>v={\pi }/{3}\;</math>, but is under the
+
-
<math>x</math>
+
-
-axis, also has a cosine value of
+
-
<math>{1}/{2}\;</math>
+
-
(same
+
-
<math>x</math>
+
-
-coordinate).
+
-
 
+
-
 
+
[[Image:4_4_1_b.gif|center]]
[[Image:4_4_1_b.gif|center]]
-
There are thus two angles,
+
There are thus two angles, <math>v=\pi/3</math> and <math>v=2\pi - \pi/3 = 5\pi/3</math> which have their cosine value equal to 1/2.
-
<math>v={\pi }/{3}\;</math>
+
-
and
+
-
<math>v=2\pi -{\pi }/{3}\;={5\pi }/{3}\;</math>
+
-
which have their cosine value equal to
+
-
<math>\frac{1}{2}</math>.
+

Version vom 13:07, 10. Okt. 2008

The easiest angle to find is \displaystyle v = \pi/3 in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive x-axis as \displaystyle v=\pi/3, but is under the x-axis, also has a cosine value of 1/2 (same x-coordinate).

There are thus two angles, \displaystyle v=\pi/3 and \displaystyle v=2\pi - \pi/3 = 5\pi/3 which have their cosine value equal to 1/2.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:1b“