Lösung 4.2:5b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
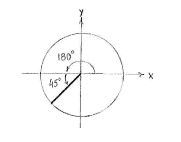
| - | If we draw the angle | + | If we draw the angle <math>225^{\circ} = 180^{\circ} + 45^{\circ}</math> on a unit circle, we see that it makes an angle of <math>45^{\circ}</math> with the negative ''x''-axis. |
| - | <math> | + | |
| - | on a unit circle, we see that it makes an angle of | + | |
| - | <math> | + | |
| - | with the negative | + | |
| - | + | ||
| - | -axis. | + | |
[[Image:4_2_5_b1.gif|center]] | [[Image:4_2_5_b1.gif|center]] | ||
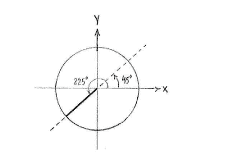
| - | This means that | + | This means that <math>\tan 225^{\circ}</math>, which is the slope of the line that makes an angle of <math>45^{\circ}</math> with the positive ''x''-axis, equals <math>\tan 45^{\circ}</math>, because the line which makes an angle of <math>45^{\circ}</math> has the same slope, |
| - | <math>\ | + | |
| - | <math> | + | |
| - | with the positive | + | |
| - | + | ||
| - | -axis, equals | + | |
| - | <math>\ | + | |
| - | <math> | + | |
| - | has the same slope | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\tan 225^{\circ} = \tan 45^{\circ} = \frac{\sin 45^{\circ}}{\cos 45^{\circ}} = \frac{\dfrac{1}{\sqrt{2}}}{\dfrac{1}{\sqrt{2}}} = 1\,\textrm{.}</math>}} | ||
[[Image:4_2_5_b2.gif|center]] | [[Image:4_2_5_b2.gif|center]] | ||
Version vom 11:08, 9. Okt. 2008
If we draw the angle \displaystyle 225^{\circ} = 180^{\circ} + 45^{\circ} on a unit circle, we see that it makes an angle of \displaystyle 45^{\circ} with the negative x-axis.
This means that \displaystyle \tan 225^{\circ}, which is the slope of the line that makes an angle of \displaystyle 45^{\circ} with the positive x-axis, equals \displaystyle \tan 45^{\circ}, because the line which makes an angle of \displaystyle 45^{\circ} has the same slope,