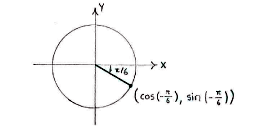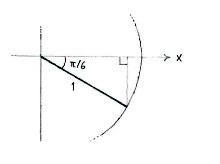Lösung 4.2:3f

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
The point on the unit circle which corresponds to the angle
+
The point on the unit circle which corresponds to the angle <math>-\pi/6</math> lies in the fourth quadrant.
-
<math>-{\pi }/{6}\;</math>
+
-
lies in the fourth quadrant.
+
-
[[Image:4_2_3_f1.gif]]
+
[[Image:4_2_3_f1.gif||center]]
-
As usual,
+
As usual, <math>\cos (-\pi/6)</math> gives the ''x''-coordinate of the point of intersection between the angle's line and the unit circle. In order to determine this point, we introduce an auxiliary triangle in the fourth quadrant.
-
<math>\cos \left( -{\pi }/{6}\; \right)</math>
+
-
gives the
+
-
<math>x</math>
+
-
-coordinate of the point of intersection between the angle's line and the unit circle. In order to determine this point, we introduce an auxiliary triangle in the fourth quadrant.
+
-
[[Image:4_2_3_f2.gif]]
+
[[Image:4_2_3_f2.gif||center]]
We can determine the edges in this triangle by simple trigonometry and then translate these over to the point's coordinates.
We can determine the edges in this triangle by simple trigonometry and then translate these over to the point's coordinates.
-
[[Image:4_2_3_f3.gif]]
+
{| width="100%"
 +
|width="50%" align="center"|[[Image:4_2_3_f3.gif]]
 +
|width="50%" align="left"|<math>\begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align}</math>
 +
|}
-
The coordinates of the point of intersection are
+
The coordinates of the point of intersection are <math>(\sqrt{3}/2,-1/2)</math> and in particular <math>\cos (-\pi/6) = \sqrt{3}/2\,</math>.
-
<math>\left( \frac{\sqrt{3}}{2} \right.,\left. -\frac{1}{2} \right)</math>
+
-
and in particular
+
-
<math>\cos \left( -{\pi }/{6}\; \right)=\frac{\sqrt{3}}{2}</math>.
+

Version vom 08:21, 9. Okt. 2008

The point on the unit circle which corresponds to the angle \displaystyle -\pi/6 lies in the fourth quadrant.

As usual, \displaystyle \cos (-\pi/6) gives the x-coordinate of the point of intersection between the angle's line and the unit circle. In order to determine this point, we introduce an auxiliary triangle in the fourth quadrant.

We can determine the edges in this triangle by simple trigonometry and then translate these over to the point's coordinates.

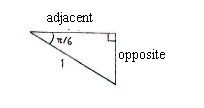
Image:4_2_3_f3.gif \displaystyle \begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align}

The coordinates of the point of intersection are \displaystyle (\sqrt{3}/2,-1/2) and in particular \displaystyle \cos (-\pi/6) = \sqrt{3}/2\,.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:3f“