Lösung 4.2:2b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | In this right-angled triangle, the opposite and the hypotenuse are given. This means that we can directly set up a relation for the sine of the angle ''v'', | |
| - | + | {| width="100%" | |
| - | + | |width="50%" align="center"|<math>\sin v = \frac{70}{110}\,\textrm{.}</math> | |
| - | + | |width="50%" align="center"|[[Image:4_2_2_b.gif]] | |
| - | + | |} | |
| - | <math>\ | + | |
| - | + | ||
The right-hand side in this equation can be simplified, so that we get | The right-hand side in this equation can be simplified, so that we get | ||
| - | + | {{Displayed math||<math>\sin v = \frac{7}{11}\,\textrm{.}</math>}} | |
| - | <math>\ | + | |
Version vom 14:29, 8. Okt. 2008
In this right-angled triangle, the opposite and the hypotenuse are given. This means that we can directly set up a relation for the sine of the angle v,
| \displaystyle \sin v = \frac{70}{110}\,\textrm{.} | 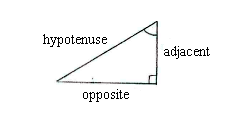
|
The right-hand side in this equation can be simplified, so that we get
