Lösung 4.2:1d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
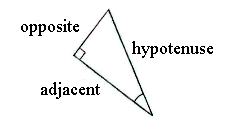
| + | The side marked ''x'' is the hypotenuse in the right-angled triangle and the side of length 16 is the adjacent to the angle of 20°. | ||
| + | |||
[[Image:4_2_1_d.gif|center]] | [[Image:4_2_1_d.gif|center]] | ||
| - | + | By writing the quotient for <math>\cos 20^{\circ}</math>, we obtain the relation | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | By writing the quotient for | + | |
| - | <math>\ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\cos 20^{\circ} = \frac{16}{x}</math>}} | ||
and this gives | and this gives | ||
| - | + | {{Displayed math||<math>x = \frac{16}{\cos20^{\circ}}\quad ({}\approx 17\textrm{.}0)\,\textrm{.}</math>}} | |
| - | <math>x=\frac{16}{\ | + | |
Version vom 14:10, 8. Okt. 2008
The side marked x is the hypotenuse in the right-angled triangle and the side of length 16 is the adjacent to the angle of 20°.
By writing the quotient for \displaystyle \cos 20^{\circ}, we obtain the relation
and this gives