Lösung 4.1:4c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
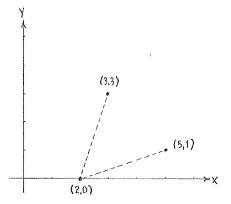
Let the point on the x-axis have coordinates
+
Let the point on the ''x''-axis have coordinates <math>(x,0)</math>, where ''x'' is an unknown number. Then, using the distance formula, the distance from the point
-
<math>\left( x \right.,\left. 0 \right)</math>, where x is an unknown number. Then, using the distance formula, the distance from the point
+
<math>(x,0)</math> to <math>(3,3)</math> and <math>(5,1)</math> is given by
-
<math>\left( x \right.,\left. 0 \right)</math>
+
-
to
+
-
<math>\left( 3 \right.,\left. 3 \right)</math>
+
-
and
+
-
<math>\left( 5 \right.,\left. 1 \right)</math>
+
-
is given by
+
 +
{{Displayed math||<math>\sqrt{(x-3)^2+(0-3)^2}\qquad\text{and}\qquad \sqrt{(x-5)^2+(0-1)^2}\,\textrm{,}</math>}}
-
<math>\sqrt{\left( x-3 \right)^{2}+\left( 0-3 \right)^{2}}</math>
+
respectively. Because these two distances should be the same, we get the equation
-
and
+
-
<math>\sqrt{\left( x-5 \right)^{2}+\left( 0-1 \right)^{2}}</math>
+
-
 
+
-
 
+
-
Because these two distances should be the same, we get the equation
+
-
 
+
-
 
+
-
<math>\sqrt{\left( x-3 \right)^{2}+9}=\sqrt{\left( x-5 \right)^{2}+1}</math>
+
 +
{{Displayed math||<math>\sqrt{(x-3)^2+9} = \sqrt{(x-5)^2+1}</math>}}
or, if we take the square, so as to get rid of the square root sign,
or, if we take the square, so as to get rid of the square root sign,
 +
{{Displayed math||<math>(x-3)^2 + 9 = (x-5)^2+1\,\textrm{.}</math>}}
-
<math>\left( x-3 \right)^{2}+9=\left( x-5 \right)^{2}+1</math>
+
Now, expand the squares and collect together all the terms onto one side,
 +
{{Displayed math||<math>\begin{align}
 +
& x^2-6x+9+9 = x^2-10x+25+1\\[5pt]
 +
&\quad\Leftrightarrow\quad 4x-8=0\,\textrm{.}
 +
\end{align}</math>}}
-
Now, expand the squares and collect together all the terms onto one side:
+
This gives that <math>x=2</math>, i.e. the point on the ''x''-axis is <math>(2,0)\,</math>.
-
<math>\begin{align}
 
-
& x^{2}-6x+9+9=x^{2}-10x+25+1 \\
 
-
& \Leftrightarrow \quad 4x-8=0 \\
 
-
\end{align}</math>
 
- 
- 
-
This gives that
 
-
<math>x=\text{2}</math>, i.e. the point on the x-axis is
 
-
<math>\left( 2 \right.,\left. 0 \right)</math>.
 
- 
- 
-
{{NAVCONTENT_START}}
 
[[Image:4_1_4_c-1(2).gif|center]]
[[Image:4_1_4_c-1(2).gif|center]]
-
{{NAVCONTENT_STOP}}
+
As a final step, we check that we have calculated correctly and that the distances really are the same. The distance between <math>(2,0)</math> and <math>(3,3)</math>
-
 
+
-
As a final step, we check that we have calculated correctly and that the distances really are the same. The distance between
+
-
<math>\left( 2 \right.,\left. 0 \right)</math>
+
-
and
+
-
<math>\left( 3 \right.,\left. 3 \right)</math>
+
is
is
 +
{{Displayed math||<math>\sqrt{(3-2)^2 + (3-0)^2} = \sqrt{1^2+3^2} = \sqrt{1+9} = \sqrt{10}</math>}}
-
<math>\sqrt{\left( 3-2 \right)^{2}+\left( 3-0 \right)^{2}}=\sqrt{1^{2}+3^{2}}=\sqrt{1+9}=\sqrt{10}</math>
+
and the distance between <math>(2,0)</math> and <math>(5,1)</math> is
-
 
+
-
 
+
-
and the distance between
+
-
<math>\left( 2 \right.,\left. 0 \right)</math>
+
-
and
+
-
<math>\left( 5 \right.,\left. 1 \right)</math>
+
-
is
+
-
 
+
-
<math>\sqrt{\left( 5-2 \right)^{2}+\left( 1-0 \right)^{2}}=\sqrt{3^{2}+1^{2}}=\sqrt{9+1}=\sqrt{10}</math>
+
{{Displayed math||<math>\sqrt{(5-2)^2 + (1-0)^2} = \sqrt{3^2 + 1^2} = \sqrt{9+1} = \sqrt{10}\,\textrm{.}</math>}}
-
NOTE: Although we squared our root equation, it is not in fact necessary to test the solution for that reason, because the expressions under the root signs are sums of squares which are never negative and therefore cannot give rise to so-called false roots.
+
Note: Although we squared our root equation, it is not in fact necessary to test the solution for that reason, because the expressions under the root signs are sums of squares which are never negative and therefore cannot give rise to so-called spurious roots.

Version vom 10:43, 7. Okt. 2008

Let the point on the x-axis have coordinates \displaystyle (x,0), where x is an unknown number. Then, using the distance formula, the distance from the point \displaystyle (x,0) to \displaystyle (3,3) and \displaystyle (5,1) is given by

Vorlage:Displayed math

respectively. Because these two distances should be the same, we get the equation

Vorlage:Displayed math

or, if we take the square, so as to get rid of the square root sign,

Vorlage:Displayed math

Now, expand the squares and collect together all the terms onto one side,

Vorlage:Displayed math

This gives that \displaystyle x=2, i.e. the point on the x-axis is \displaystyle (2,0)\,.



As a final step, we check that we have calculated correctly and that the distances really are the same. The distance between \displaystyle (2,0) and \displaystyle (3,3) is

Vorlage:Displayed math

and the distance between \displaystyle (2,0) and \displaystyle (5,1) is

Vorlage:Displayed math


Note: Although we squared our root equation, it is not in fact necessary to test the solution for that reason, because the expressions under the root signs are sums of squares which are never negative and therefore cannot give rise to so-called spurious roots.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:4c“