Lösung 4.1:4a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
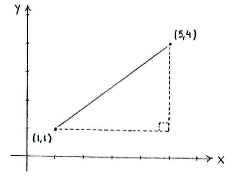
If we draw in the points in a coordinate system, we can see the line between the points as the hypotenuse in an imaginary right-angled triangle, where the opposite and adjacent are parallel with the
+
If we draw in the points in a coordinate system, we can see the line between the points as the hypotenuse in an imaginary right-angled triangle, where the opposite and adjacent are parallel with the ''x''- and ''y''-axes, respectively.
-
<math>x</math>
+
-
- and
+
-
<math>y</math>
+
-
-axes.
+
-
{{NAVCONTENT_START}}
 
[[Image:4_1_4_a-1(2)_1.gif|center]]
[[Image:4_1_4_a-1(2)_1.gif|center]]
-
In this triangle, it is easy to measure the lengths of the opposite and the adjacent, which are simply the distances between the points in the
 
-
<math>x</math>
 
-
-
 
-
<math>y</math>
 
-
-directions.
 
-
[[Image:4_1_4_a-1(2)_2.gif|center]]
 
 +
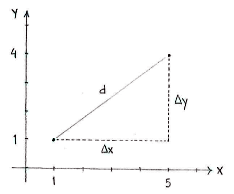
In this triangle, it is easy to measure the lengths of the opposite and the adjacent, which are simply the distances between the points in the ''x''- and ''y''-directions, respectively.
-
{{NAVCONTENT_STOP}}
 
-
Using Pythagoras' theorem, we can then calculate the length of the hypotenuse, which is also the distance between the points:
+
{| align="center"
 +
|align="center"|[[Image:4_1_4_a-1(2)_2.gif|center]]
 +
|-
 +
|align="center"|<small>∆''x''&nbsp;=&nbsp;5&nbsp;-&nbsp;1&nbsp;=&nbsp;4 &nbsp;and&nbsp; ∆''y''&nbsp;=&nbsp;4&nbsp;-&nbsp;1&nbsp;=&nbsp;3</small>
 +
|}
-
<math>\begin{align}
+
Using the Pythagorean theorem, we can then calculate the length of the hypotenuse, which is also the distance between the points:
-
& d=\sqrt{\left( \Delta x \right)^{2}+\left( \Delta y \right)^{2}}=\sqrt{4^{2}+3^{2}} \\
+
-
& =\sqrt{16+9}=\sqrt{25}=5 \\
+
-
\end{align}</math>
+
 +
{{Displayed math||<math>\begin{align}
 +
d &= \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{4^2+3^2}\\[5pt]
 +
&= \sqrt{16+9} = \sqrt{25} = 5\,\textrm{.}
 +
\end{align}</math>}}
-
NOTE: In general, the distance between two points
 
-
<math>\left( x \right.,\left. y \right)</math>
 
-
and
 
-
<math>\left( a \right.,\left. b \right)</math>
 
-
is given by the formula
 
 +
Note: In general, the distance between two points <math>(x,y)</math> and <math>(a,b)</math> is given by the formula
-
<math>d=\sqrt{\left( x-a \right)^{2}+\left( y-b \right)^{2}}</math>
+
{{Displayed math||<math>d = \sqrt{(x-a)^2 + (y-b)^2}\,\textrm{.}</math>}}

Version vom 10:40, 3. Okt. 2008

If we draw in the points in a coordinate system, we can see the line between the points as the hypotenuse in an imaginary right-angled triangle, where the opposite and adjacent are parallel with the x- and y-axes, respectively.



In this triangle, it is easy to measure the lengths of the opposite and the adjacent, which are simply the distances between the points in the x- and y-directions, respectively.


∆x = 5 - 1 = 4  and  ∆y = 4 - 1 = 3


Using the Pythagorean theorem, we can then calculate the length of the hypotenuse, which is also the distance between the points:

Vorlage:Displayed math


Note: In general, the distance between two points \displaystyle (x,y) and \displaystyle (a,b) is given by the formula

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:4a“