Lösung 2.2:6e
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
The lines have a point of intersection at that point which simultaneously satisfies the equations of both lines | The lines have a point of intersection at that point which simultaneously satisfies the equations of both lines | ||
| - | {{ | + | {{Abgesetzte Formel||<math>2x+y-1=0\qquad\text{and}\qquad y-2x-2=0\,\textrm{.}</math>}} |
If we make ''y'' the subject of the second equation <math>y=2x+2</math> and substitute it into the first equation, we obtain an equation which only contains ''x'', | If we make ''y'' the subject of the second equation <math>y=2x+2</math> and substitute it into the first equation, we obtain an equation which only contains ''x'', | ||
| - | {{ | + | {{Abgesetzte Formel||<math>2x+(2x+2)-1=0\quad\Leftrightarrow\quad 4x+1=0\,,</math>}} |
which gives that <math>x=-1/4\,</math>. Then, from the relation <math>y=2x+2</math>, we obtain <math>y = 2\cdot(-1/4)+2 = 3/2\,</math>. | which gives that <math>x=-1/4\,</math>. Then, from the relation <math>y=2x+2</math>, we obtain <math>y = 2\cdot(-1/4)+2 = 3/2\,</math>. | ||
Version vom 08:29, 22. Okt. 2008
The lines have a point of intersection at that point which simultaneously satisfies the equations of both lines
| \displaystyle 2x+y-1=0\qquad\text{and}\qquad y-2x-2=0\,\textrm{.} |
If we make y the subject of the second equation \displaystyle y=2x+2 and substitute it into the first equation, we obtain an equation which only contains x,
| \displaystyle 2x+(2x+2)-1=0\quad\Leftrightarrow\quad 4x+1=0\,, |
which gives that \displaystyle x=-1/4\,. Then, from the relation \displaystyle y=2x+2, we obtain \displaystyle y = 2\cdot(-1/4)+2 = 3/2\,.
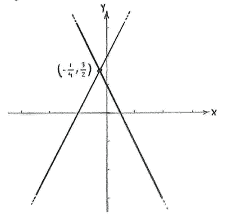
The point of intersection is \displaystyle \bigl(-\tfrac{1}{4},\tfrac{3}{2}\bigr).
We check for safety's sake that \displaystyle \bigl(-\tfrac{1}{4},\tfrac{3}{2}\bigr)
really satisfies both equations:
- 2x + y - 1 = 0: \displaystyle \quad\textrm{LHS} = 2\cdot\bigl(-\tfrac{1}{4}\bigr) + \tfrac{3}{2} - 1 = -\tfrac{1}{2} + \tfrac{3}{2} - \tfrac{2}{2} = 0 = \textrm{RHS.}
- y - 2x - 2 = 0: \displaystyle \quad\textrm{LHS} = \tfrac{3}{2}-2\cdot\bigl(-\tfrac{1}{4}\bigr)-2 = \tfrac{3}{2} + \tfrac{1}{2} - \tfrac{4}{2} = 0 = \textrm{RHS.}