Lösung 2.2:6a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 3: Zeile 3:
If the point of intersection has coordinates (''x'',''y''), then
If the point of intersection has coordinates (''x'',''y''), then
-
{{Displayed math||
+
{{Abgesetzte Formel||
<math>\left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.</math>}}
<math>\left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.</math>}}
If we substitute <math>y=0</math> into the first equation, we obtain
If we substitute <math>y=0</math> into the first equation, we obtain
-
{{Displayed math||<math>0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}</math>}}
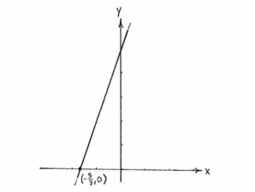
The point of intersection is (-5/3,0).
The point of intersection is (-5/3,0).

Version vom 08:29, 22. Okt. 2008

According to the definition, the point of intersection between two lines is that point which lies on both lines; it must therefore satisfy the equations of both lines.

If the point of intersection has coordinates (x,y), then

\displaystyle \left\{\begin{align} y&=3x+5\,,\\ y&=0\,\textrm{.}\qquad\quad\text{(x-axis)}\end{align}\right.

If we substitute \displaystyle y=0 into the first equation, we obtain

\displaystyle 0=3x+5,\qquad\text{i.e.}\quad x=-\frac{5}{3}\,\textrm{.}

The point of intersection is (-5/3,0).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:6a“