Lösung 2.3:8a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
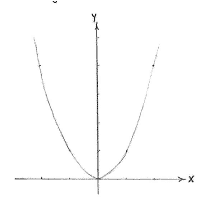
| - | The curve | + | The curve <math>y=x^{2}</math> is a parabola with a minimum at the origin according to the figure below on the left and, compared with that curve, <math>y=x^{2}+1</math> |
| - | <math>y=x^{2}</math> | + | is the same curve but with the number 1 added to the ''y''-coordinate of each point, i.e. the parabola is shifted one unit up in the ''y''-direction. |
| - | is a parabola with a minimum at the origin according to the figure below on the left and, compared with that curve, | + | |
| - | <math>y=x^{2}+1</math> | + | |
| - | is the same curve but with the number | + | |
| - | + | ||
| - | added to the | + | |
| - | + | ||
| - | -coordinate of | + | |
| - | + | ||
| - | -direction. | + | |
| - | [[Image:2_3_8_a.gif|center]] | + | {| align="center" |
| + | |align="center"|[[Image:2_3_8_a-1.gif|center]] | ||
| + | | width="10px"| | ||
| + | |align="center"|[[Image:2_3_8_a-1.gif|center]] | ||
| + | |- | ||
| + | |align="center"|<small>The graph of ''f''(''x'') = ''x''²</small> | ||
| + | || | ||
| + | |align="center"|<small>The graph of ''f''(''x'') = ''x''² + 1</small> | ||
| + | |} | ||
Version vom 12:29, 29. Sep. 2008
The curve \displaystyle y=x^{2} is a parabola with a minimum at the origin according to the figure below on the left and, compared with that curve, \displaystyle y=x^{2}+1 is the same curve but with the number 1 added to the y-coordinate of each point, i.e. the parabola is shifted one unit up in the y-direction.
| The graph of f(x) = x² | The graph of f(x) = x² + 1 |