Lösung 2.2:9b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
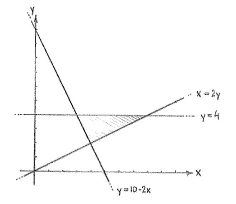
A first step is to draw the lines so that we get an overview of how the triangles look.
+
A first step is to draw the lines so that we get an overview of how the triangle looks like.
 +
 
[[Image:2_2_9_b-1(3).gif|center]]
[[Image:2_2_9_b-1(3).gif|center]]
-
The corner points of the triangle are the intersection points of the lines and we obtain those more
 
-
exactly by choosing the equations of the lines in pairs and solving the resulting system of equations.
 
-
<math>\left\{ \begin{matrix}
+
The corner points of the triangle are the intersection points of the lines and we obtain those more exactly by choosing the equations of the lines in pairs and solving the resulting system of equations,
-
x=2y \\
+
-
y=4 \\
+
-
\end{matrix} \right.</math>
+
-
+
-
<math>\left\{ \begin{matrix}
+
-
x=2y \\
+
-
y=10-2y \\
+
-
\end{matrix} \right.</math>
+
-
and
+
-
<math>\left\{ \begin{matrix}
+
-
y=4 \\
+
-
y=10-2y \\
+
-
\end{matrix} \right.</math>
+
 +
{{Displayed math||<math>\left\{\begin{align} x&=2y,\\ y&=4,\end{align}\right.\qquad
 +
\left\{\begin{align} x&=2y,\\ y&=10-2y,\end{align}\right.\qquad
 +
\text{and}\qquad
 +
\left\{\begin{align} y&=4,\\ y&=10-2y\,\textrm{.}\end{align}\right.</math>}}
 +
 +
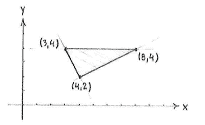
The first system of equations has the solution <math>(x,y) = (8,4)</math>, the second system has the solution <math>(x,y) = (4,2)</math>
 +
and the third system <math>(x,y) = (3,4)\,</math>.
-
The first system of equations has the solution
 
-
<math>\left( x,y \right)=\left( \text{8},\text{4} \right)</math>, the other has the solution
 
-
<math>\left( x,y \right)=\left( \text{4},\text{2} \right)\text{ }</math>
 
-
and the third
 
-
<math>\left( x,y \right)=\left( \text{3},\text{4} \right)</math>.
 
[[Image:2_2_9_b-2(3).gif|center]]
[[Image:2_2_9_b-2(3).gif|center]]
-
If we go back to the area of the triangle, which is given by the formula
 
-
Area=
 
-
<math>\frac{1}{2}</math>
 
-
(base)∙(height),
 
-
we are completely free to choose which edge of the triangle we take as the base. Because one of the edges is parallel with the x-axis, it seems best to choose that one as the base, since then we can easily read off the length of the base and the height as the difference in coordinates of the corner points.
+
If we go back to the area of the triangle, which is given by the formula
-
[[Image:2_2_9_b-3(3).gif|center]]
+
{{Displayed math||<math>\text{Area} = \tfrac{1}{2}\cdot\text{(base)}\cdot\text{(height),}</math>}}
 +
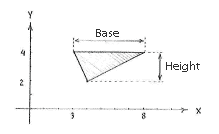
we are completely free to choose which edge of the triangle we take as the base. Because one of the edges is parallel with the ''x''-axis, it seems best to choose that one as the base, since then we can easily read off the length of the base and the height as the difference in coordinates of the corner points.
-
The base is given as the horizontal distance between
 
-
<math>\left( \text{3},\text{4} \right)\text{ }</math>
 
-
and
 
-
<math>\text{ }\left( \text{8},\text{4} \right)</math>
 
 +
[[Image:2_2_9_b-3(3).gif|center]]
-
base=
 
-
<math>\text{8}-\text{3}=\text{5}</math>
 
 +
The base is given as the horizontal distance between (3,4) and (8,4),
-
and we obtain the height in the same way as the difference in the
+
{{Displayed math||<math>\text{base} = 8-3 = 5</math>}}
-
<math>y</math>
+
-
-direction between the base at
+
-
<math>y=\text{4 }</math>
+
-
and the corner point
+
-
<math>\left( \text{4},\text{2} \right)</math>,
+
-
height=
+
and we obtain the height in the same way as the difference in the ''y''-direction between the base at <math>y=4</math> and the corner point (4,2),
-
<math>\text{4}-\text{2}=\text{2}</math>.
+
-
The area of the triangle is
+
{{Displayed math||<math>\text{height} = 4-2 = 2\,\textrm{.}</math>}}
-
Area =
+
The area of the triangle is
-
<math>\frac{1}{2}</math>
+
-
(base)∙(height)=
+
-
<math>\frac{1}{2}\centerdot 5\centerdot 5</math>
+
-
=
+
{{Displayed math||<math>\text{Area} = \tfrac{1}{2}\cdot\text{(base)}\cdot\text{(height)} = \tfrac{1}{2}\cdot 5\cdot 2 = 5\,\text{u.a.}</math>}}
-
<math>\text{5}</math>
+
-
area units.
+

Version vom 14:14, 24. Sep. 2008

A first step is to draw the lines so that we get an overview of how the triangle looks like.



The corner points of the triangle are the intersection points of the lines and we obtain those more exactly by choosing the equations of the lines in pairs and solving the resulting system of equations,

Vorlage:Displayed math

The first system of equations has the solution \displaystyle (x,y) = (8,4), the second system has the solution \displaystyle (x,y) = (4,2) and the third system \displaystyle (x,y) = (3,4)\,.



If we go back to the area of the triangle, which is given by the formula

Vorlage:Displayed math

we are completely free to choose which edge of the triangle we take as the base. Because one of the edges is parallel with the x-axis, it seems best to choose that one as the base, since then we can easily read off the length of the base and the height as the difference in coordinates of the corner points.



The base is given as the horizontal distance between (3,4) and (8,4),

Vorlage:Displayed math

and we obtain the height in the same way as the difference in the y-direction between the base at \displaystyle y=4 and the corner point (4,2),

Vorlage:Displayed math

The area of the triangle is

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:9b“