Lösung 2.2:6d

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
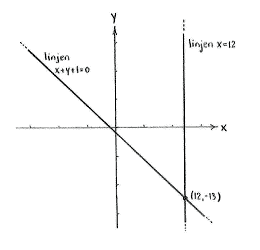
At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines:
+
At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines,
 +
{{Displayed math||<math>x+y+1=0\qquad\text{and}\qquad x=12\,\textrm{.}</math>}}
-
<math>x+y+1=0</math>
+
We obtain the solution to this system of equations by substituting <math>x=12</math>
-
and
+
-
<math>x=12</math>.
+
-
 
+
-
We obtain the solution to this system of equations by substituting
+
-
<math>x=12</math>
+
into the first equation
into the first equation
 +
{{Displayed math||<math>12+y+1=0\quad\Leftrightarrow\quad y=-13\,\textrm{,}</math>}}
-
<math>12+y+1=0\ \Leftrightarrow \ y=-13</math>
+
which gives us the point of intersection as (12,-13).
-
 
+
-
which gives us the point of intersection as
+
-
<math>\left( 12 \right.,\left. -13 \right)</math>.
+
-
 
+
-
{{NAVCONTENT_START}}
 
-
[[Image:2_2_6_d.gif|center]]
 
-
{{NAVCONTENT_STOP}}
+
<center>[[Image:2_2_6_d.gif|center]]</center>

Version vom 13:14, 24. Sep. 2008

At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines,

Vorlage:Displayed math

We obtain the solution to this system of equations by substituting \displaystyle x=12 into the first equation

Vorlage:Displayed math

which gives us the point of intersection as (12,-13).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:6d“