Lösung 4.4:3d

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.4:3d moved to Solution 4.4:3d: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
First, we observe from the unit circle that the equation has two solutions for
-
<center> [[Image:4_4_3d.gif]] </center>
+
<math>0^{\circ }\le \text{3}x\le \text{36}0^{\circ }</math>,
-
{{NAVCONTENT_STOP}}
+
 
 +
 
 +
<math>3x=15^{\circ }</math>
 +
and
 +
<math>3x=180^{\circ }-15^{\circ }=165^{\circ }</math>
 +
 
[[Image:4_4_3_d.gif|center]]
[[Image:4_4_3_d.gif|center]]
 +
 +
This means that all of the equation's solutions are
 +
 +
 +
<math>3x=15^{\circ }+n\centerdot 360^{\circ }</math>
 +
and
 +
<math>3x=165^{\circ }+n\centerdot 360^{\circ }</math>
 +
 +
 +
for all integers
 +
<math>n</math>, i.e.
 +
 +
 +
<math>x=5^{\circ }+n\centerdot 120^{\circ }</math>
 +
and
 +
<math>x=55^{\circ }+n\centerdot 120^{\circ }</math>

Version vom 09:57, 1. Okt. 2008

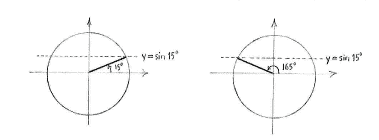
First, we observe from the unit circle that the equation has two solutions for \displaystyle 0^{\circ }\le \text{3}x\le \text{36}0^{\circ },


\displaystyle 3x=15^{\circ } and \displaystyle 3x=180^{\circ }-15^{\circ }=165^{\circ }


This means that all of the equation's solutions are


\displaystyle 3x=15^{\circ }+n\centerdot 360^{\circ } and \displaystyle 3x=165^{\circ }+n\centerdot 360^{\circ }


for all integers \displaystyle n, i.e.


\displaystyle x=5^{\circ }+n\centerdot 120^{\circ } and \displaystyle x=55^{\circ }+n\centerdot 120^{\circ }

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:3d“