Lösung 4.2:9

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.2:9 moved to Solution 4.2:9: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
If we introduce the dashed triangle below, the distance as the crow flies between
-
<center> [[Image:4_2_9-1(3).gif]] </center>
+
<math>\text{A}</math>
-
{{NAVCONTENT_STOP}}
+
and
-
{{NAVCONTENT_START}}
+
<math>\text{B}</math>
-
<center> [[Image:4_2_9-2(3).gif]] </center>
+
is equal to the triangle's hypotenuse,
-
{{NAVCONTENT_STOP}}
+
<math>c</math>.
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:4_2_9-3(3).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
[[Image:4_2_9_1.gif|center]]
[[Image:4_2_9_1.gif|center]]
 +
 +
One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since Pythagoras' theorem then gives
 +
 +
 +
<math>c^{2}=a^{2}+b^{2}</math>
 +
 +
 +
In turn, we can determine the opposite and adjacent by introducing another triangle
 +
<math>\text{APR}</math>, where
 +
<math>\text{R}</math>
 +
is the point on the line
 +
<math>\text{PQ}</math>
 +
which the dashed triangle's side of length
 +
<math>a</math>
 +
cuts the line.
 +
[[Image:4_2_9_2.gif|center]]
[[Image:4_2_9_2.gif|center]]
 +
 +
Because we know that
 +
<math>\text{AP}=\text{4}</math>
 +
and the angle at P, simple trigonometry shows that
 +
<math>x</math>
 +
and
 +
<math>y</math>
 +
are given by
 +
 +
 +
<math>\begin{align}
 +
& x=4\sin 30^{\circ }=4\centerdot \frac{1}{2}=2, \\
 +
& y=4\cos 30^{\circ }=4\centerdot \frac{\sqrt{3}}{2}=2\sqrt{3} \\
 +
\end{align}</math>
 +
 +
 +
We can now start to look for the solution. Since
 +
<math>x</math>
 +
and
 +
<math>y</math>
 +
have been calculated, we can determine
 +
<math>a</math>
 +
and b by considering the horizontal and vertical distances in the figure.
 +
 +
[[Image:4_2_9_3.gif|center]]
[[Image:4_2_9_3.gif|center]]
 +
 +
<math>a=x+5=2+5=7</math>
 +
 +
<math>b=12-y=12-2\sqrt{3}</math>
 +
 +
 +
With a and
 +
<math>b</math>
 +
given, Pythagoras' theorem leads to
 +
 +
 +
<math>\begin{align}
 +
& c=\sqrt{a^{2}+b^{2}}=\sqrt{7^{2}+\left( 12-2\sqrt{3} \right)^{2}} \\
 +
& =\sqrt{49+\left( 12^{2}-2\centerdot 12\centerdot 2\sqrt{3}+\left( 2\sqrt{3} \right)^{2} \right)} \\
 +
& =\sqrt{205-38\sqrt{3}}\quad \approx \quad 11.0\quad \text{km}\text{.} \\
 +
\end{align}</math>

Version vom 09:58, 29. Sep. 2008

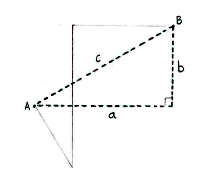
If we introduce the dashed triangle below, the distance as the crow flies between \displaystyle \text{A} and \displaystyle \text{B} is equal to the triangle's hypotenuse, \displaystyle c.


One way to determine the hypotenuse is to know the triangle's opposite and adjacent sides, since Pythagoras' theorem then gives


\displaystyle c^{2}=a^{2}+b^{2}


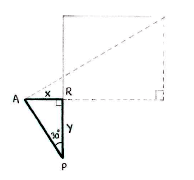
In turn, we can determine the opposite and adjacent by introducing another triangle \displaystyle \text{APR}, where \displaystyle \text{R} is the point on the line \displaystyle \text{PQ} which the dashed triangle's side of length \displaystyle a cuts the line.

Because we know that \displaystyle \text{AP}=\text{4} and the angle at P, simple trigonometry shows that \displaystyle x and \displaystyle y are given by


\displaystyle \begin{align} & x=4\sin 30^{\circ }=4\centerdot \frac{1}{2}=2, \\ & y=4\cos 30^{\circ }=4\centerdot \frac{\sqrt{3}}{2}=2\sqrt{3} \\ \end{align}


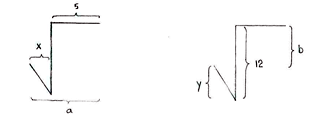
We can now start to look for the solution. Since \displaystyle x and \displaystyle y have been calculated, we can determine \displaystyle a and b by considering the horizontal and vertical distances in the figure.


\displaystyle a=x+5=2+5=7

\displaystyle b=12-y=12-2\sqrt{3}


With a and \displaystyle b given, Pythagoras' theorem leads to


\displaystyle \begin{align} & c=\sqrt{a^{2}+b^{2}}=\sqrt{7^{2}+\left( 12-2\sqrt{3} \right)^{2}} \\ & =\sqrt{49+\left( 12^{2}-2\centerdot 12\centerdot 2\sqrt{3}+\left( 2\sqrt{3} \right)^{2} \right)} \\ & =\sqrt{205-38\sqrt{3}}\quad \approx \quad 11.0\quad \text{km}\text{.} \\ \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:9“