Lösung 4.2:8

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.2:8 moved to Solution 4.2:8: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
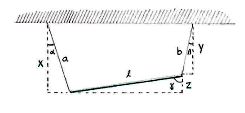
We start by drawing three auxiliary triangles, and calling the three vertical sides
-
<center> [[Image:4_2_8-1(2).gif]] </center>
+
<math>x,\ y</math>
-
{{NAVCONTENT_STOP}}
+
and
-
{{NAVCONTENT_START}}
+
<math>z</math>, as shown in the figure.
-
<center> [[Image:4_2_8-2(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
[[Image:4_2_8.gif|center]]
[[Image:4_2_8.gif|center]]
 +
 +
Using the definition of cosine, we can work out
 +
<math>x\text{ }</math>
 +
and
 +
<math>y</math>
 +
from
 +
 +
 +
<math>x=a\cos \alpha </math>
 +
 +
 +
<math>y=b\cos \beta </math>
 +
 +
and, for the same reason, we know that
 +
<math>z\text{ }</math>
 +
satisfies the relation
 +
 +
 +
<math>z=l\cos \gamma </math>
 +
 +
 +
In addition, we know that the lengths
 +
<math>x,\ y</math>
 +
and
 +
<math>z</math>
 +
satisfy the equality
 +
 +
 +
<math>z=x-y</math>
 +
 +
 +
If we substitute in the expressions for
 +
<math>x,\ y</math>
 +
and
 +
<math>z</math>, we obtain the trigonometric equation
 +
 +
 +
<math>l\cos \gamma =a\cos \alpha -b\cos \beta </math>
 +
 +
 +
where
 +
<math>\gamma </math>
 +
is the only unknown.

Version vom 09:40, 29. Sep. 2008

We start by drawing three auxiliary triangles, and calling the three vertical sides \displaystyle x,\ y and \displaystyle z, as shown in the figure.


Using the definition of cosine, we can work out \displaystyle x\text{ } and \displaystyle y from


\displaystyle x=a\cos \alpha


\displaystyle y=b\cos \beta

and, for the same reason, we know that \displaystyle z\text{ } satisfies the relation


\displaystyle z=l\cos \gamma


In addition, we know that the lengths \displaystyle x,\ y and \displaystyle z satisfy the equality


\displaystyle z=x-y


If we substitute in the expressions for \displaystyle x,\ y and \displaystyle z, we obtain the trigonometric equation


\displaystyle l\cos \gamma =a\cos \alpha -b\cos \beta


where \displaystyle \gamma is the only unknown.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:8“