Lösung 4.2:7

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.2:7 moved to Solution 4.2:7: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
If extend the line
-
<center> [[Image:4_2_7-1(2).gif]] </center>
+
<math>\text{AB}</math>
-
{{NAVCONTENT_STOP}}
+
to a point
-
{{NAVCONTENT_START}}
+
<math>\text{D}</math>
-
<center> [[Image:4_2_7-2(2).gif]] </center>
+
opposite
-
{{NAVCONTENT_STOP}}
+
<math>\text{C}</math>, we will get the right-angled triangle shown below, where the distance
 +
<math>x</math>
 +
between
 +
<math>\text{C}</math>
 +
and
 +
<math>\text{D}</math>
 +
is the desired distance.
[[Image:4_2_7_1.gif|center]]
[[Image:4_2_7_1.gif|center]]
 +
 +
The information in the exercise can be summarized by considering the two triangles
 +
<math>\text{ACD}</math>
 +
and
 +
<math>\text{BCD}</math>, and setting up relations for the tangents that the angles
 +
<math>\text{3}0^{\circ }</math>
 +
and
 +
<math>\text{45}^{\circ }</math>
 +
gives rise to,
 +
 +
[[Image:4_2_7_2.gif|center]]
[[Image:4_2_7_2.gif|center]]
 +
 +
<math>x=\left( 100+y \right)\tan 30^{\circ }=\left( 100+y \right)\frac{1}{\sqrt{3}}</math> <math>x=y\centerdot \tan 45^{\circ }=y\centerdot 1</math>
 +
 +
 +
 +
where
 +
<math>y</math>
 +
is the distance between B and D.
 +
 +
The second relation above gives that
 +
<math>y=x</math>
 +
and substituting this into the first relation gives
 +
 +
 +
<math>x=\left( 100+x \right)\frac{1}{\sqrt{3}}</math>
 +
 +
 +
Multiplying both sides by
 +
<math>\sqrt{3}</math>
 +
gives
 +
 +
 +
<math>\sqrt{3}x=100+x</math>
 +
 +
 +
moving all the x-terms to the left-hand side gives
 +
 +
 +
<math>\left( \sqrt{3}-1 \right)x=100</math>
 +
 +
 +
The answer is
 +
 +
 +
<math>x=\frac{100}{\sqrt{3}-1}\ \text{m}\quad \approx \quad \text{136}\text{.6}\ \text{m}</math>

Version vom 08:55, 29. Sep. 2008

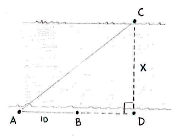
If extend the line \displaystyle \text{AB} to a point \displaystyle \text{D} opposite \displaystyle \text{C}, we will get the right-angled triangle shown below, where the distance \displaystyle x between \displaystyle \text{C} and \displaystyle \text{D} is the desired distance.


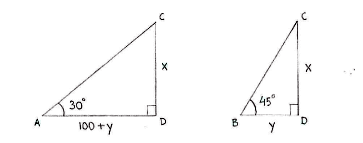
The information in the exercise can be summarized by considering the two triangles \displaystyle \text{ACD} and \displaystyle \text{BCD}, and setting up relations for the tangents that the angles \displaystyle \text{3}0^{\circ } and \displaystyle \text{45}^{\circ } gives rise to,


\displaystyle x=\left( 100+y \right)\tan 30^{\circ }=\left( 100+y \right)\frac{1}{\sqrt{3}} \displaystyle x=y\centerdot \tan 45^{\circ }=y\centerdot 1


where \displaystyle y is the distance between B and D.

The second relation above gives that \displaystyle y=x and substituting this into the first relation gives


\displaystyle x=\left( 100+x \right)\frac{1}{\sqrt{3}}


Multiplying both sides by \displaystyle \sqrt{3} gives


\displaystyle \sqrt{3}x=100+x


moving all the x-terms to the left-hand side gives


\displaystyle \left( \sqrt{3}-1 \right)x=100


The answer is


\displaystyle x=\frac{100}{\sqrt{3}-1}\ \text{m}\quad \approx \quad \text{136}\text{.6}\ \text{m}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:7“