Lösung 2.3:9c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 2.3:9c moved to Solution 2.3:9c: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
To determine all the points on the curve
-
<center> [[Image:2_3_9c.gif]] </center>
+
<math>y=3x^{2}-12x+9</math>
-
{{NAVCONTENT_STOP}}
+
which also lie on the
 +
<math>x</math>
 +
-axis we substitute the equation of the
 +
<math>x</math>
 +
-axis i.e.
 +
<math>y=0</math>
 +
in the equation of the curve and obtain that
 +
<math>x</math>
 +
must satisfy
 +
 
 +
 
 +
<math>3x^{2}-12x+9=0</math>
 +
 
 +
 
 +
After dividing by
 +
<math>3</math>
 +
and completing the square the right-hand side is
 +
 
 +
 
 +
<math>x^{2}-4x+3=\left( x-2 \right)^{2}-2^{2}+3=\left( x-2 \right)^{2}-1</math>
 +
 
 +
 
 +
and thus the equation has solutions
 +
 
 +
 
 +
<math>x=2\pm 1,</math>
 +
i.e.
 +
<math>x=2-1=1</math>
 +
and
 +
<math>x=2+1=3.</math>
 +
 
 +
 
 +
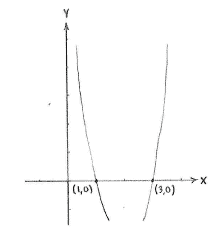
The points where the curve cut the
 +
<math>x</math>
 +
-axis are
 +
 
 +
 
 +
<math>\left( 1 \right.,\left. 0 \right)</math>
 +
and
 +
<math>\left( 3 \right.,\left. 0 \right)</math>
 +
 
 +
 
 +
 
[[Image:2_3_9_c.gif|center]]
[[Image:2_3_9_c.gif|center]]

Version vom 12:11, 21. Sep. 2008

To determine all the points on the curve \displaystyle y=3x^{2}-12x+9 which also lie on the \displaystyle x -axis we substitute the equation of the \displaystyle x -axis i.e. \displaystyle y=0 in the equation of the curve and obtain that \displaystyle x must satisfy


\displaystyle 3x^{2}-12x+9=0


After dividing by \displaystyle 3 and completing the square the right-hand side is


\displaystyle x^{2}-4x+3=\left( x-2 \right)^{2}-2^{2}+3=\left( x-2 \right)^{2}-1


and thus the equation has solutions


\displaystyle x=2\pm 1, i.e. \displaystyle x=2-1=1 and \displaystyle x=2+1=3.


The points where the curve cut the \displaystyle x -axis are


\displaystyle \left( 1 \right.,\left. 0 \right) and \displaystyle \left( 3 \right.,\left. 0 \right)


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:9c“