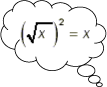3.1 Wurzeln
Aus Online Mathematik Brückenkurs 1
K |
K (small fixes) |
||
| Zeile 8: | Zeile 8: | ||
{{Info| | {{Info| | ||
| - | ''' | + | '''Contents:''' |
| - | * | + | *Square roots and ''n'''th roots |
*Manipulating roots | *Manipulating roots | ||
}} | }} | ||
| Zeile 21: | Zeile 21: | ||
*That the square root of a number denotes the positive root. | *That the square root of a number denotes the positive root. | ||
*How to manipulate roots in the simplification of expressions containing roots. | *How to manipulate roots in the simplification of expressions containing roots. | ||
| - | *To recognise when the methods of manipulating roots are valid. (Non-negative | + | *To recognise when the methods of manipulating roots are valid. (Non-negative arguments). |
*How to simplify expressions containing quadratic roots in the denominator. | *How to simplify expressions containing quadratic roots in the denominator. | ||
| - | *When the n | + | *When the ''n'''th root of a negative number is defined (''n'' odd). |
}} | }} | ||
| - | == | + | == Square roots == |
[[Bild:rotbubbla.gif|right]] | [[Bild:rotbubbla.gif|right]] | ||
| Zeile 35: | Zeile 35: | ||
<div class="regel"> | <div class="regel"> | ||
| - | + | The square root <math>\sqrt{a}</math> means '''the non-negative number''' that multiplied by | |
itself gives <math>a,</math> i.e. the non-negative solution to the equation <math>x^2 = a</math>. | itself gives <math>a,</math> i.e. the non-negative solution to the equation <math>x^2 = a</math>. | ||
| Zeile 121: | Zeile 121: | ||
</div> | </div> | ||
| - | Note that, unlike | + | Note that, unlike square roots, cube roots are also defined for negative numbers. |
| - | For any positive integers <math>n</math> one can define the <math>n</math> | + | For any positive integers <math>n</math> one can define the <math>n</math>'th root of a number <math>a</math> as |
* if <math>n</math> is even and <math>a\ge0</math> then <math>\sqrt[\scriptstyle n]{a}</math> is the non-negative number that when multiplied by itself <math>n</math> times gives <math>a</math>, | * if <math>n</math> is even and <math>a\ge0</math> then <math>\sqrt[\scriptstyle n]{a}</math> is the non-negative number that when multiplied by itself <math>n</math> times gives <math>a</math>, | ||
| Zeile 142: | Zeile 142: | ||
</div> | </div> | ||
| - | For <math>n</math> | + | For <math>n</math>'th roots the same rules apply as for quadratic roots if <math>a, \, b \ge 0</math>. Note that if <math>n</math> is odd these methods apply even for negative <math>a</math> and <math>b</math>, that is, for all real numbers <math>a</math> and <math>b</math>. |
<div class="regel"> | <div class="regel"> | ||
| Zeile 241: | Zeile 241: | ||
== Rational root expressions == | == Rational root expressions == | ||
| - | When roots appear in a rational expression one often | + | When roots appear in a rational expression one often wants to avoid roots in the denominator (because it is difficult with hand calculations to divide by irrational numbers). By multiplying the numerator and denominator by <math> \sqrt{2} </math> for example, one obtains |
{{Fristående formel||<math>\frac{1}{\sqrt{2}} | {{Fristående formel||<math>\frac{1}{\sqrt{2}} | ||
| Zeile 249: | Zeile 249: | ||
which usually is preferable. | which usually is preferable. | ||
| - | In other cases, you can take advantage of the difference of two squares method, <math>(a+b)(a-b) = a^2 – b^2</math>. One multiplies the numerator and denominator by the denominator´s “conjugate” and the root sign is eliminated from the denominator by squaring, as in the following, | + | In other cases, you can take advantage of the difference of two squares method, <math>(a+b)(a-b) = a^2 – b^2</math>. One multiplies the numerator and denominator by the denominator´s “conjugate” expression and the root sign is eliminated from the denominator by squaring, as in the following, |
{{Fristående formel||<math>\begin{align*} | {{Fristående formel||<math>\begin{align*} | ||
| Zeile 303: | Zeile 303: | ||
'''Keep in mind that: ''' | '''Keep in mind that: ''' | ||
| - | + | The square root of a number is always non-negative (that is, positive or zero)! | |
| - | Rules for roots are actually special case of laws of exponents . | + | Rules for roots are actually a special case of laws of exponents . |
For example: <math>\sqrt{x}=x^{1/2}</math>. | For example: <math>\sqrt{x}=x^{1/2}</math>. | ||
Version vom 08:37, 19. Aug. 2008
Contents:
- Square roots and n'th roots
- Manipulating roots
Learning outcomes:
After this section, you will have learned:
- How to calculate the square root of some simple integers.
- That the square root of a negative number has not been defined.
- That the square root of a number denotes the positive root.
- How to manipulate roots in the simplification of expressions containing roots.
- To recognise when the methods of manipulating roots are valid. (Non-negative arguments).
- How to simplify expressions containing quadratic roots in the denominator.
- When the n'th root of a negative number is defined (n odd).
Square roots
The well-known symbol \displaystyle \sqrt{a}, the square root of \displaystyle a, is used to describe the number that when multiplied by itself gives \displaystyle a. However, one has to be a little more precise in defining this symbol.
The equation \displaystyle x^2 = 4 has two solutions \displaystyle x = 2 and \displaystyle x = -2, since both \displaystyle 2\cdot 2 = 4 and \displaystyle (-2)\cdot(-2) = 4. It would then be logical to suppose that \displaystyle \sqrt{4} can be either \displaystyle -2 or \displaystyle 2, i.e. \displaystyle \sqrt{4}= \pm 2, but \displaystyle \sqrt{4} only denotes the positive number \displaystyle 2.
The square root \displaystyle \sqrt{a} means the non-negative number that multiplied by itself gives \displaystyle a, i.e. the non-negative solution to the equation \displaystyle x^2 = a.
Square root of \displaystyle a can also be written as \displaystyle a^{1/2}.
It is therefore wrong to state that \displaystyle \sqrt{4}= \pm 2, but correct to state that the equation \displaystyle x^2 = 4 has the solution \displaystyle x = \pm 2.
Example 1
- \displaystyle \sqrt{0}=0 \quad because \displaystyle 0^2 = 0 \cdot 0 = 0 and \displaystyle 0 is not negative.
- \displaystyle \sqrt{100}=10 \quad since \displaystyle 10^2 = 10 \cdot 10 = 100 and \displaystyle 10 is a positive number.
- \displaystyle \sqrt{0{,}25}=0{,}5 \quad since \displaystyle 0{,}5^2 = 0{,}5 \cdot 0{,}5 = 0{,}25 and \displaystyle 0{,}5 is positive.
- \displaystyle \sqrt{2} \approx 1{,}4142 \quad since \displaystyle 1{,}4142 \cdot 1{,}4142 \approx 2 and \displaystyle 1{,}4142 is positive.
- The equation \displaystyle x^2=2 has the solutions \displaystyle x=\sqrt{2} \approx 1{,}414 and \displaystyle x = -\sqrt{2} \approx -1{,}414.
- \displaystyle \sqrt{-4}\quad is not defined, since there is no real number \displaystyle x that satisfies \displaystyle x^2=-4.
- \displaystyle \sqrt{(-7)^2} = 7 \quad because \displaystyle \sqrt{(-7)^2} = \sqrt{(-7) \cdot (-7)} = \sqrt{49} = \sqrt{ 7 \cdot 7} = 7.
When taking square roots, it is useful to know some methods of calculation. As \displaystyle \sqrt{a} = a^{1/2} we can use the laws of exponents as "laws of roots". For example, we have Vorlage:Fristående formel In this way we obtain the following rules for quadratic roots, which apply to all real numbers \displaystyle a, b \ge 0:
( We must however, in the above division, assume as always that b is not 0.)
Example 2
- \displaystyle \sqrt{64\cdot 81} = \sqrt{64}\cdot \sqrt{81} = 8\cdot 9 = 72
- \displaystyle \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}
- \displaystyle \sqrt{18} \cdot \sqrt{2} = \sqrt{18 \cdot 2} = \sqrt{36} = 6
- \displaystyle \frac{\sqrt{75}}{\sqrt{3}} = \sqrt{\frac{75}{3}} = \sqrt{25} = 5
- \displaystyle \sqrt{12} = \sqrt{ 4 \cdot 3 } = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}
Note that the above calculations assume that \displaystyle a and \displaystyle b \ge 0. If \displaystyle a and \displaystyle b are negative (< 0) then \displaystyle \sqrt{a} and \displaystyle \sqrt{b} are not defined as real numbers. It is tempting to write , for example,
but something here cannot be right. The explanation is that \displaystyle \sqrt{-1} is not a real number, which means the laws of roots discussed above may not be used.
Higher order roots
The cube root of a number \displaystyle a is defined as the number that multiplied by itself three times gives \displaystyle a, and is denoted as \displaystyle \sqrt[\scriptstyle 3]{a}.
Example 3
- \displaystyle \sqrt[\scriptstyle 3]{8} = 2 \quad as \displaystyle 2 \cdot 2 \cdot 2=8.
- \displaystyle \sqrt[\scriptstyle 3]{0{,}027} = 0{,}3 \quad since \displaystyle 0{,}3 \cdot 0{,}3 \cdot 0{,}3 = 0{,}027.
- \displaystyle \sqrt[\scriptstyle 3]{-8} = -2 \quad because \displaystyle (-2) \cdot (-2) \cdot (-2)= -8.
Note that, unlike square roots, cube roots are also defined for negative numbers.
For any positive integers \displaystyle n one can define the \displaystyle n'th root of a number \displaystyle a as
- if \displaystyle n is even and \displaystyle a\ge0 then \displaystyle \sqrt[\scriptstyle n]{a} is the non-negative number that when multiplied by itself \displaystyle n times gives \displaystyle a,
- if \displaystyle n is odd, \displaystyle \sqrt[\scriptstyle n]{a} is the number that when multiplied by itself \displaystyle n times gives \displaystyle a.
The root \displaystyle \sqrt[\scriptstyle n]{a} can also be written as \displaystyle a^{1/n}.
Example 4
- \displaystyle \sqrt[\scriptstyle 4]{625} = 5\quad since \displaystyle 5 \cdot 5 \cdot 5 \cdot 5 = 625.
- \displaystyle \sqrt[\scriptstyle 5]{-243} = -3\quad because \displaystyle (-3) \cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = -243.
- \displaystyle \sqrt[\scriptstyle 6]{-17}\quad is not defined as \displaystyle 6 is even and \displaystyle -17 is a negative number.
For \displaystyle n'th roots the same rules apply as for quadratic roots if \displaystyle a, \, b \ge 0. Note that if \displaystyle n is odd these methods apply even for negative \displaystyle a and \displaystyle b, that is, for all real numbers \displaystyle a and \displaystyle b.
Simplification of expressions containing roots
Often, one can significantly simplify expressions containing roots by using the usual methods for roots . As is also the case when using the laws of exponents, it is desirable to reduce expressions into as "small" roots as possible. For example, it is a good idea to do the following
because it helps simplification as we see here
By rewriting expressions containing roots in terms of "small" roots one can also sum roots of "the same kind", e.g.
Example 5
- \displaystyle \frac{\sqrt{8}}{\sqrt{18}} = \frac{\sqrt{2 \cdot 4}}{\sqrt{2 \cdot 9}} = \frac{\sqrt{2 \cdot 2 \cdot 2}}{\sqrt{2 \cdot 3 \cdot 3}} = \frac{\sqrt{2 \cdot 2^2}}{\sqrt{2 \cdot 3^2}} = \frac{2\sqrt{2}}{3\sqrt{2}} = \frac{2}{3}
- \displaystyle \frac{\sqrt{72}}{6} = \frac{\sqrt{8 \cdot 9}}{ 2 \cdot 3} = \frac{\sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}}{ 2 \cdot 3} = \frac{\sqrt{2^2 \cdot 3^2 \cdot 2}}{ 2 \cdot 3} = \frac{2 \cdot 3\sqrt{2}}{2 \cdot 3} = \sqrt{2}
- \displaystyle \sqrt{45} + \sqrt{20}
= \sqrt{9\cdot5} + \sqrt{4\cdot5}
= \sqrt{3^2\cdot5} + \sqrt{2^2\cdot5}
= 3\sqrt{5} + 2\sqrt{5}\vphantom{\bigl(}
\displaystyle \phantom{\sqrt{45} + \sqrt{20}\vphantom{\bigl(}}{} = (3+2)\sqrt{5} = 5\sqrt{5} - \displaystyle \sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}
= \sqrt{5 \cdot 10} + 2\sqrt{3} -\sqrt{2 \cdot 16}
+ \sqrt{3 \cdot 9}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5 \cdot 2 \cdot 5} + 2\sqrt{3} -\sqrt{2 \cdot 4 \cdot 4} + \sqrt{3 \cdot 3 \cdot 3}\vphantom{a^{b^c}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5^2 \cdot 2 } + 2\sqrt{3} -\sqrt{2^2 \cdot 2^2 \cdot 2} + \sqrt{3 \cdot 3^2}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = 5\sqrt{2} +2\sqrt{3} - 2 \cdot 2\sqrt{2} + 3\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = (5-4)\sqrt{2} + (2+3)\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{2} + 5\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}} - \displaystyle \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{12} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3 \cdot 4} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3} \cdot \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2 \cdot 2} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2} \cdot \sqrt[\scriptstyle3]{2} } \cdot \displaystyle \frac{\sqrt[\scriptstyle3]{2}}{ \sqrt[\scriptstyle3]{2}} = \frac{ 2\cdot\sqrt[\scriptstyle3]{2} }{ 2 } = \sqrt[\scriptstyle3]{2}
- \displaystyle (\sqrt{3} + \sqrt{2}\,)(\sqrt{3} - \sqrt{2}\,) = (\sqrt{3}\,)^2-(\sqrt{2}\,)^2 = 3-2 = 1 where we have used the difference of two squares \displaystyle (a+b)(a-b) = a^2 - b^2 with \displaystyle a=\sqrt{3} and \displaystyle b=\sqrt{2}.
Rational root expressions
When roots appear in a rational expression one often wants to avoid roots in the denominator (because it is difficult with hand calculations to divide by irrational numbers). By multiplying the numerator and denominator by \displaystyle \sqrt{2} for example, one obtains
which usually is preferable.
In other cases, you can take advantage of the difference of two squares method, \displaystyle (a+b)(a-b) = a^2 – b^2. One multiplies the numerator and denominator by the denominator´s “conjugate” expression and the root sign is eliminated from the denominator by squaring, as in the following,
Example 6
- \displaystyle \frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} = \frac{10\sqrt{15}}{5} = 2\sqrt{15}
- \displaystyle \frac{1+\sqrt{3}}{\sqrt{2}} = \frac{(1+\sqrt{3})\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} = \frac{\sqrt{2}+\sqrt{6}}{2}
- \displaystyle \frac{3}{\sqrt{2}-2} = \frac{3(\sqrt{2}+2)}{(\sqrt{2}-2)(\sqrt{2}+2)} = \frac{3\sqrt{2}+6}{(\sqrt{2}\,)^2-2^2} = \frac{3\sqrt{2}+6}{2-4} = -\frac{3\sqrt{2}+6}{2}
- \displaystyle \frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}
= \frac{\sqrt{2}\,(\sqrt{6}-\sqrt{3}\,)}{(\sqrt{6}+\sqrt{3}\,)
(\sqrt{6}-\sqrt{3}\,)}
= \frac{\sqrt{2}\,\sqrt{6}-\sqrt{2}\,\sqrt{3}}{(\sqrt{6}\,)^2
-(\sqrt{3}\,)^2}\vphantom{\Biggl(}
\displaystyle \phantom{\frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}\vphantom{\Biggl(}}{} = \frac{\sqrt{2}\,\sqrt{2\cdot 3}-\sqrt{2}\,\sqrt{3}}{6-3} = \frac{2\sqrt{3}-\sqrt{2}\,\sqrt{3}}{3} = \frac{(2-\sqrt{2}\,)\sqrt{3}}{3} \vphantom{\displaystyle\frac{a^{\textstyle b^{\textstyle c}}}{b}}
Study advice
Basic and final tests
After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.
Keep in mind that:
The square root of a number is always non-negative (that is, positive or zero)!
Rules for roots are actually a special case of laws of exponents .
For example: \displaystyle \sqrt{x}=x^{1/2}.
Reviews
For those of you who want to deepen your studies or need more detailed explanations consider the following references
Learn more about square roots in the English Wikipedia
How do we know that the root of 2 is not a fraction?
Useful web sites
How to find the root of a number, without the help of calculators?